戻る
  
50年をかえりみる

磁性研究50年のあゆみ

芳田 奎

〈東京理科大学理工学部 278千葉県野田市山崎2641〉

第2次世界戦争終結後，戦後の復興期を経て，固体物理の研究は戦前の研究を受け継ぎ，その路線に沿って進歩発展し今日に到っている．この稿では，固体物理の戦後50年にわたる進展の経過を磁性研究に重点を置いて，理論の立場から概観する．

§1.　はじめに--研究の発展を支えてきたもの--

戦後50年の長い年月にわたって研究を支え，その発展を促進してきたものは，新しい実験技術の開発である．戦後新しく導入された中性子線回折と磁気共鳴吸収の実験手段は戦後の磁性研究に大きな影響を与えた．磁気共鳴吸収は物質中の電子スピンの共鳴吸収(ESR)と核スピンの共鳴吸収(NMR)からなる．これら二つの研究手段はスピンの動的振舞に対する知識をも提供する．このため，今日においても，磁性研究の強力な手段となっている．
これら二つの実験手段に，NMRと同様に核スピンを通して周囲の電子状態を探るMssbauer効果を用いる実験方法が加った．これは1960年MssbauerによるMssbauer効果の発見を契機として開発された．さらに1970年代後半にはm-中間子を用いたmSRと呼ばれる研究手段が開発され，NMR, Mssbauer効果と同様に物質内部の電子状態の研究に広く用いられ，成果を挙げている．

新しい実験装置としては第2種超伝導体の研究によって開発された超伝導磁石がある．これによって，従来2テスラ以下に抑えられていた電磁石による静的磁場が10テスラから20テスラ近くまで引き上げられた．これに対して，大電流を流すことによって更に大きな磁場を発生する装置が我が国で開発され（約50テスラ，持続時間10−3秒から200テスラ，持続時間10−6秒），物質の磁気測定の磁場範囲を画期的に拡大した．

実験装置の革命的開発としては稀釈冷凍機を挙げねばならない．これは液体4Heに3Heを稀釈させるときの吸熱反応を利用するもので，この冷凍機によって絶対温度10 K位から出発して数mKの温度までの冷却が可能になった．

以上のほか新しい測定手段の開発は数多く存在する．超伝導Josephson効果の発見に伴って開発された微小な磁場の精密測定に利用されるSQUID (superconducting quantum interference device)の開発や，また近くは走査型電子顕微鏡(STM)， トンネル分光(STS)の技術開発などがあって，微妙な精密測定に利用されている．

以上述べてきたように，過去50年間に非常に多くの技術革新があり，実験装置もこれにより精密化している．現在における物性研究，磁性研究はこのような新しい実験装置に支えられ進展を続けている．

§2.　絶縁体磁性体，とくに反強磁性の研究

以下，戦後に出現した注目すべき研究を順を追ってみてゆくことにする．戦後に発表された論文のうち私の興味を惹きつけた最初の論文はNel1) (1948)のフェリ磁性の論文である．NelはここでMOFe2O3なる化学式をもつ絶縁体イオン結晶の示す強磁性の簡明な説明を与えた．MはMn, Fe, Co など2価の鉄族イオンである．フェライトは立方晶のスピネル構造をもつ結晶で酸素は面心格子を形成し，金属イオンはその隙間の格子点を占める．その格子点には周囲の4個の酸素によって正四面体的に囲まれたAの位置と，6個の酸素によってほぼ正八面体的に囲まれたBの位置がある．スピネルには正スピネルと逆スピネル構造があり，フェライトではMがMnのときは正スピネル，MがFe, Co, Ni, Cuの場合は逆スピネル構造をとる．逆スピネルでは3価の鉄イオンはAの位置を，残りのFe3+とM2+とがBの位置を占める． Nelの着想は，Aの位置の磁性イオンのスピンとBの位置のイオンのスピンとの間に強い反強磁性交換相互作用が働く，と考えたことである．この考えに立つと，AのスピンとBのスピンは低温で互いに反平行に向き合うことになる．単位胞中のAの格子点の数は8個，Bの格子点の数は2倍の16個ある．したがって，この強い反強磁性相互作用によりB格子点上のスピンの半数はA格子点のスピンによって打消されるが，残り半数のM2+のスピンは平行スピンとして残ることになる．Nelはこのようにしてフェライトの強磁性を説明し，このような互いに反平行に揃った2種類のスピンが部分的に打消し，残りの平行スピンから発生する強磁性をフェリ磁性と名付けた．このようなフェリ磁性の他の代表例はイットリウム鉄ガーネット(YIG)及びYを稀土類イオンで置換したガーネットに見られる．
Nelの研究によってフェライトを構成する鉄イオンではその軌道角運動量は結晶電場によって殆ど消失し，その磁気モーメントはすべて3d電子のスピンに由来していること，但しFe2+, Co2+では多少とも軌道角運動量からの寄与があることなどが明らかにされた．このNelの研究を契機として，フェライトは絶縁体強磁性材料として応用面でも大きな貢献をすることになった．

Nelの論文に続いて注目すべき研究はOak RidgeでなされたNaCl構造をもつ酸化物MO (MはMn, Fe, Co, Ni)の中性子線回折の実験である．最初にShullとSmart2) (1949)はMnOの低温（115 K以下）のMn2+イオンのスピン構造を決定した．これが中性子線回折による研究の最初の成果である．この構造ではO2−の両側のMn2+のスピンがすべて互いに反平行に揃ったスピン構造をしている．このことはこれら二つのM2+のスピン間に強い反強磁性的相互作用が働くことを意味する．この相互作用は中央に介在したO2−によって媒介されて生じるもので，超交換相互作用と呼ばれる．フェライトのA, B格子点間にも酸素が介在している．超交換相互作用は三つのイオン(M2+−O2−−M2+)のクラスターを対象に3次の摂動から生じることがAnderson3) (1950)によって示されたが，その後3次摂動のプロセスが詳細に検討され，交換相互作用を発生する多くの機構が可能であることが明らかになり，この相互作用発生の本質の把握が難しい状況になってきた．このような困難を回避して，超交換相互作用の由来の本質を明らかにしたのはAnderson4) (1959)である．

Andersonは磁性イオンの化合物である絶縁体はWilsonの意味での絶縁体ではなくて，Mottの絶縁体であることに注目する．磁性イオンは不完全3d殻をもつから，バンド計算では3dバンドは不完全で金属になる筈である．これを絶縁体に保っているのは磁性イオン内の3d電子間に働くクーロンの反撥力である．この同じ格子点の電子間のクーロン積分をUとすると，Mott絶縁体はこのUが3d電子を隣の磁性イオンの格子点に移動させる行列要素|t |よりもかなり大きいときに実現する．Andersonは3d電子の軌道と隣り合った酸素の2p電子の軌道間に共有結合的混成を考える．このとき，3d軌道の波動関数には隣り合った酸素の2p電子の軌道が混成している．このため一つの3d電子から隣の磁性イオンの3d軌道への遷移が可能になる．この遷移行列要素をtとすれば，2次摂動によって隣り合った磁性イオンのスピン間に

で与えられるスピン相互作用が発生することになる．これがAndersonによって与えられた超交換相互作用であり，Mott絶縁体を形成する磁性イオンのスピン間のスピン相互作用の起源である．

1950年代は，鉄族イオンを含む化合物絶縁体の常磁性，反強磁性の研究が強力に進められた時代である．ここでは比熱，帯磁率の静的研究のほか，戦後に新しく導入された磁気共鳴吸収の方法によって磁性体のスピンの動的性質が研究され，マイクロ波による吸収線の共鳴振動数，吸収曲線の形，その線幅の理論が展開された．この間，Bloembergen-Purcell-Pound5) (1948)の理論展開，Van Vleck及びAnderson-Weiss6) (1953)の線幅の理論，これらを統一的に記述する久保-富田7) (1954)の理論は特に重要である．

なお，絶縁体反強磁性の研究としては結晶場による異方性の起源，スピン間の異方性相互作用の研究，3d電子のdg軌道の縮退を解く結晶Jahn-Teller効果の研究，さらには反強磁性スピン波理論の展開などを挙げなければならない．反強磁性スピン波理論の展開はAnderson8) (1952)及び久保9) (1952)によって行われた．Andersonはスピン波理論に立って反強磁性の基底状態の研究，特に量子効果の研究を行った．また，久保はスピン波理論によって比熱，帯磁率，部分格子の磁化の低温における温度変化を計算した．反強磁性体（3次元）では，Heisenbergハミルトニアンが示唆する全スピンSTot＝0のスピン一重項の状態ではなく，互いに逆方向に分極したスピンをもつ部分格子からなる状態（これを特にNel状態と呼ぶ）が実現している．Andersonの論文では，何故このNel状態が実現するのかという基本的問題，即ち「対称性の破れ」の問題が議論された．

§3.　s-d交換相互作用

戦前のSlater-Stonerの金属強磁性理論に対して，Zener10) (1951)はいわゆるs-d模型なるものを提案した．Zenerは金属強磁性の主な磁性の担い手の3d電子のほかに，結晶中を殆ど自由に動き廻る4s電子の存在に注目し，遍歴4s電子と局在3d電子のスピン間に働く交換相互作用が強磁性の主要な原因と考えた．この模型を現象論的に扱うと自由エネルギーは次のように表現される．

ここにSs, Sdは4s及び3d電子の単位体積当りのスピン偏極を表わす．a, gはそれぞれをスピン偏極させるために必要なエネルギーの増加を表わす定数で，ともに帯磁率の逆数で与えられる．bはs-d間の交換相互作用の係数で，一応正と考える．(2)式を最小にするエネルギーは

と与えられ，bの正負にかかわらずb2/a−g＞0の限り，3d電子の強磁性が出現する．

Zener模型では3d電子は局在スピンと考えているし，3d電子間の交換相互作用は重視しない．したがって，この模型は鉄族金属の場合にはあてはまらない．この場合，低温の電子比熱がTに比例することからも，3d電子はまちがいなく遍歴電子であり，3d電子間の交換相互作用が強磁性の原因と考えるのがより自然である．

Zenerのs-d模型が成立するのは稀土類金属の場合と磁性稀薄合金の場合と考えられる．稀土類金属の場合，磁性イオンの磁気モーメントは不完全4f電子が担う．4f軌道はイオン殻の内側にあって，隣り合った格子上の4f電子の間に働く直接の相互作用は小さいと考えられる．また，CuMnのような稀薄合金では磁性を坦うMn2+イオンの濃度が稀薄なために，平均のMn2+-Mn2+間の距離は大きくなっているからである．

Zenerの(2)式は現象論的に過ぎる．s-d模型は正確にはミクロなハミルトニアンに基づかねばならない．金属伝導電子と局在スピンとの間の交換相互作用は

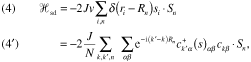
の形に書くことができる．ここにSnはn番目の格子点に局在するスピン，ri , si は伝導電子の座標とスピンを表わす．vは格子点当りの体積で，全体積V と全格子数N の比で与えられる．(4')は(4)を第2量子化の形式に書き直したものであり，,は波数k' , kスピン成分が＋又は−の伝導電子の生成，消滅演算子である．Jはs-d交換積分を表わす．全ハミルトニアンはこれと伝導電子の運動エネルギーとの和によって与えられる．

自由な伝導電子系（Fermi球）に対して(4)式を摂動として扱えば，2次摂動項として局在スピンSn 間に伝導電子を媒介として次の交換相互作用が導かれる．

ここにNeは伝導電子数，eFはFermiエネルギー，kFはFermi波数である．F(x)は

なる関数である．(5)式は局在スピンの代りに核スピンに対して，Ruderman-Kittel11) (1954) によって導かれた．このときs-d交換積分J は超微細構造相互作用の係数Aで置き換えられる．糟谷12)(1956)はこのようなs-d模型に基いて稀土類金属，特にGdの強磁性を論じた．

いま一つの局在スピンに着目する．この局在スピンは伝導電子のスピンとs-d交換相互作用をもつ．この相互作用は局在スピンの廻りに伝導電子のスピン偏極の雲を誘起する．この偏極の雲の分布は(5)式と同じF (2kF|r−Rn|)で与えられる．n 格子点から離れたm 格子点上の局在スピンが電子雲の伝導電子のスピンと結合して生じた相互作用が(5)式に外ならない．このような局在スピンの廻りに発生した伝導電子のスピン偏極がs-d模型では本質的役割を演じる．

稀土類金属の磁性の研究はそう古くからのものではない．Gdの強磁性については以前から知られていたが，他の稀土類金属の磁性についての研究は1950年代に始められた．というのは化学的に同じ性質をもつ稀土類金属を分離することは難しい．純度のよい稀土類金属は専らIowa州立大学のSpeddingの研究室で作られた．この単結晶試料を用いて中性子線回折の実験が1960年代の初めにOak RidgeのWollan, Koehler, Wilkinson13)たちのグループで行われた．その結果，Gdより重い稀土類金属のスピンはヘリカル・スピン構造，あるいはヘリカル構造が異方性エネルギーによって変形した構造をとることが明らかにされた．スピンのヘリカル構造はMnO2, MnAu2などで見られ，吉森14)ら(1959)によって，その出現が予想されたものである．スピンのヘリカル構造は距離とともに振動しながら1/R 3で減衰してゆくRKKY相互作用によって安定化するものと理解される．

磁性稀薄合金の場合は，不純物スピン間に(5)式のRKKY相互作用が働くが，磁性イオンは無秩序に格子点を占拠しているので，規則正しい反強磁性スピン構造は出現しない．しかしながら一つの磁性イオンのスピンは廻りの磁性イオンのスピンとの相互作用によって，十分低温ではある方向に凍結する．この方向は磁性イオンによって異る．このような状態はスピングラスと呼ばれる．その代表はCuMn稀薄合金である．スピングラスの研究は一時期重要な研究対象として活発に研究が進められたが，ランダム系のために数学的取扱いが困難であって，いまなお完全な解決には至っていないように思われる．

以上，稀薄磁性合金の代表としてCuMnを念頭に置いてきた．ここでは自由イオンMn2+をもつ3d電子のスピンモーメントは，Cuの溶媒中ではそのまま保持されるのに対して，Al中ではそのスピンを失って単なる非磁性イオンとして振舞うことが実験的に明らかになった．このような事実を理解するためにAnderson15) (1961)は現在Anderson模型と呼ばれている次のハミルトニアンを提出した．

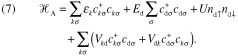
このハミルトニアンは伝導電子の運動エネルギーを表わす第1項に以下の各項を付け加えたものである．第2項は不純物磁性イオンの局在d軌道を占めるd電子のエネルギーを表わす．第3項は局在d軌道を＋，−スピンのd電子が占拠したとき，その2電子間に働くクーロン斥力ポテンシャルを表わす項である．但し，Ed＜eF, Ed+U＞eFとする．第4項は伝導電子軌道と局在d軌道の間の電子の移動を表わす．σは電子の+，−スピンを表わす．この項はs-d mixingの項と呼ばれる．もし，クーロン斥力U＝0の場合，この局在d電子軌道は伝導電子軌道と混成し，＋，−スピンの電子はこの混成軌道を均等に占拠し，局在スピンは消失する．局在スピンは第3項のクーロン斥力によって発生する．

一方，稀薄合金の電気抵抗及び磁性の研究は，1950年代の後半頃からJ. Friedel16)によって進められてきた．Friedelはこの問題を一貫して伝導電子の不純物局在ポテンシャルによる散乱問題として取扱った．不純物ポテンシャルによる散乱の結果，伝導電子はこのポテンシャルを遮蔽するために不純物の廻りに集ってくる．この遮蔽電子数をdn としたとき，このdnは散乱理論によって

で与えられる．ここにdl (eF)は，伝導電子の波動関数を不純物を中心として部分波に分解したとき，l波の受けるFermi面における位相シフトである．Z は溶質原子と溶媒原子の価電子数の差である．この法則はFriedelの和則(1958)と呼ばれ，Friedelはこの法則を彼の議論の基礎においた．

ここで，伝導電子間にクローン斥力あるいは交換相互作用を導入する．この交換相互作用が十分大きければ，不純物原子の廻りに集ってきた電荷はスピン分極を起こし，不純物は局在スピンをもつようになる．これがFriedelが考えた合金中の局在スピンの発生機構である．これに対しAnderson模型では，この遮蔽電子のスピン偏極を初めからd軌道の電子として取り入れ，これがs-d mixingによって消失すると考える．従って，Anderson模型はFriedel理論とは表裏一体をなすものと考えられる．

U が大きい場合，d軌道の電子は局在スピンをもつ．U が大きい極限ではmixing項を摂動として扱うことができる．このとき，Anderson模型はs-d模型に帰着する．ただし，s-d交換積分Jの符号は負になり，その大きさは4N |V |2/U で与えられる．

稀薄磁性合金の磁性イオンの濃度がさらに小さくなると，磁性イオン間のRKKY相互作用も無視できるようになる．このとき，近藤効果が出現する．ただし，近藤効果が出現するのはs-d交換相互作用が負の場合に限られる．従って，近藤効果の本質はAnderson模型の中に求めなくてはならない．

§4.　磁性の周辺における理論展開

1950年代から60年代の初めにかけては，磁性に限らず固体物理全分野で非常に多くの重要な理論展開があった．その最も大きな進展は超伝導理論の展開である．量子力学が完成し，これに基づく固体電子論の枠組は終戦前にすでに出来上っていたが，超伝導現象は多くの実験結果の蓄積はあったものの，ミクロの立場からの理論的理解は全く得られていなかった．これが，1957年Bardeen-Cooper-Schrieffer17)の理論によって一挙に解決されたように見えたのであるから，このBCS理論の物理学界に与えたインパクトは大変大きなものがあった．この理論を契機として超伝導現象の研究は理論の検証，精密化を目指して一段と活発化した．超伝導理論については別項で詳細な解説が行われる予定であるので，BCS理論以後の超伝導研究の発展については，ここでは触れないことにする．
BCS理論と並んで重要な超伝導の理論はGinzburg-Landau18) (1950)によって展開された．これはLandauの2次相転移の現象論を超伝導現象にそのまま適用したものである．そこでは自由エネルギーは秩序パラメータyの冪展開で与えられる．このため適用範囲は転移温度Tcの近傍の温度範囲に限られるが，二つのパラメータ即ち磁場侵入の長さlとコヒーレンスの長さx(k＝l/x)を含み，外部磁場下の超伝導体の反磁性的性質を殆ど完全に記述する．特に第2種超伝導体と呼ばれるの超伝導体では，磁場が臨界磁場Hc1を超えると磁場は(H＜Hc2)超伝導体内に糸状に侵入するが，その場合の磁束の分布を完全に記述する．このことはAbrikosov19) (1957)によって示され，この磁束の構造（三角格子）はAbrikosov構造と呼ばれている．

現在，超伝導は一応磁性とは別の分野のものとして分類されている．しかし超伝導現象は本来軌道反磁性の問題，しかも完全反磁性の問題であって，磁性研究の重要テーマと考えてしかるべきと思われる．

超伝導理論以外の研究として注目されるのは，久保20)(1957)による量子統計力学に基づく一般的立場からの線形応答理論の展開である．このいわゆる久保理論あるいは久保公式が導かれる経緯については別に解説されるので，ここでは深入りはしない．久保理論は実質的には外部磁場及び電場に対する1次の応答，すなわち帯磁率c(q, w)及び電気伝導度s(w)の表式を与える．そうは言ってもこの公式を使って実際にc, sを求めるには，また大変な苦労が必要である．この計算には以下に述べるGreen関数の方法が使われる．

この時代の重要な理論展開としては，Landau21)(1956)によるFermi液体論の展開がある．Fermi液体論はFermi粒子である3Heの液体の低温の振舞を説明するために提出されたものであるが，この理論は強い短距離斥力相互作用をもつ金属伝導電子系にも適用される．Landau理論の要点はつぎのようなものである．Fermi粒子系に粒子間に働く短距離斥力相互作用を導入すると，この相互作用によってFermi面に近いエネルギーをもつ粒子は散乱されて有限の寿命をもつ．この寿命はPauli原理のためにFermi面から測ったエネルギーeの2乗または温度の2乗に比例する．この有限寿命のために波数ベクトルkの状態は純粋の状態ではなくなる．しかし，十分低温，低エネルギー励起に対してはこの寿命は長く，その逆数は励起エネルギーに比べて十分小さいので準粒子としての記述が可能になる．これがFermi液体論が成立する所以である．準粒子系の振舞は自由粒子系と同様であるが，質量，圧縮率，スピン帯磁率は準粒子間の相互作用を表わすパラメータ（Landauパラメータ）によって繰り込まれた値に変わる．

現象論であるLandauのFermi液体論に対して，直ちにミクロの立場からこれを基礎づける研究がLuttinger22) (1960), NoziresやLandauグループの人達によって進められた．ここでは本質的には斥力相互作用を摂動とし，Feynmanダイヤグラム展開を用い，自由エネルギー，Green関数の構造を調べるのである．この理論展開はNozires23)とAbrikosov-Gorkov-Dzyaloshinski24)の教科書に詳述され，現在では多体問題を対象とする量子統計力学の最も標準的手段になっている．ここでは，しばしば時間の代りに虚数時間＝b＝/kTをもつ温度Green関数が用いられる．温度Green関数を用いたFeynmanダイヤグラム展開法は松原25)(1955)によって先鞭をつけられたもので，Landauグループはこの温度Green関数を用いて超伝導理論を展開した．

1950年代に発表された論文のうち，もう一つAnderson26)(1958)によるAnderson局在の論文に注目しなければならない．これはSi結晶中の29Siの核スピンの拡散の問題に関連して展開された理論であるが，結晶中の電子の場合，Blochの定理によって結晶全体に拡がった電子の波動関数が不純物によるランダム・ポテンシャルによって局在化するというものである．Anderson局在についての研究は，後にAnderson27)ら(1979)によるスケーリング則に基づく理論展開を契機として大きく進展し，2次元ランダム系の電気抵抗の温度変化の問題，さらには半導体不純物伝導に見られる負の磁気抵抗の問題などが解決された．半導体不純物伝導に見られる負の磁気抵抗は，戦後間もなく発見された現象で，長い間，この現象の理論的説明に苦慮してきた問題である．Anderson局在はまた量子Hall効果の問題にも重要な役割を演じる．

§5.　強い電子相関の研究

鉄，コバルト，ニッケルの金属強磁性は3d遍歴電子系を対象に，電子間の交換相互作用を平均場として取扱うSlater-Stonerの平均場理論で記述されてきた．しかし，この平均場近似では実験事実に合わない点がいくつか存在する．低温の自発磁化の温度による減少はスピン波理論が示唆するT3/2に比例すること，臨界指数，転移温度以上の帯磁率のCurie-Weiss則などが挙げられる．これらはむしろ局在スピン系を記述するHeisenberg模型によって導かれる特性である．このようなSlater-Stoner理論の欠点は，そこでは電子間相互作用を摂動で考慮した場合，摂動の2次以上の効果，すなわち電子相関の効果，もっと端的にはスピンの平均値からのゆらぎの効果を無視していることに起因している．
この電子相関の問題は1962-1963年に到って，Hubbard,28)金森29)及びGutzwiller30)によって取り上げられた．彼らの対象としたハミルトニアンは，現在HubbardにちなんでHubbardハミルトニアンと呼ばれる，次のハミルトニアンである．

第1項は遍歴電子のバンドエネルギーで，これらの電子間の相互作用としては第2項の同じ格子点上の2電子間の斥力ポテンシャルU のみを考慮する．

Hubbardは(9)式のハミルトニアンに対して2時間Green関数の運動方程式に現れる高次のGreen関数をdecoupleする近似法を用いて検討した．この理論ではU が大きくなると，電子が空孔を伝って運動する下のバンドと，既に占拠された格子点を動く上のバンドに分離し，バンド間にHubbardギャップと呼ばれるエネルギーギャップが生じる．電子数が格子点当り一つ，すなわちhalf-filledの場合にはこの状態はMott絶縁体状態に対応する．

金森は，(9)式を斥力U による2電子間の多重散乱を考慮に入れたt -マトリックス近似を用いて考察した．この近似は電子数が少ないときによい近似と考えられる．金森の結論は鉄族3dバンドのように，いくつかのバンドが関与している場合，バンド間の交換積分は重要ではなく，同じバンド内の2電子間のクーロン積分U が重要であること，このクーロン積分U は多重散乱によってUeffに還元され，U の大きい極限ではこのUeffはバンド幅によって抑えられる．強磁性は通常のバンドに対しては期待できない．強磁性が起るためには，バンド幅がかなり大きく，且つ同時にFermi面上の状態密度が局所的に大きくなっていることが必要で，Niではこの条件が満たされていることなどである．

第3番目の理論はGutzwillerによる変分理論である．Gutzwillerは変分関数として

を採用する．j0はU がゼロの自由な電子系の基底状態の波動関数，すなわち＋，−スピンの電子のFermi球を表わす．yでは同じ格子点を2電子が占拠する重みはg に減少されていて，このg が変分パラメータである．問題は変分関数(10)によるHubbardハミルトニアンの期待値を計算することである．これは非常に難しい問題で，Gutzwillerはこれを確率論的に評価する．この近似はGutzwiller近似と呼ばれる．この近似の上に立ってGutzwillerはNiの強磁性を論じ，金森理論と同様の結論を得た．

一方，Brinkman-Rice31) (1970)はn＝1，丁度half-filledの場合をGutzwiller近似の範囲内で検討し，U がその臨界値Ucに達すると，金属-非金属転移，すなわちMott転移が起こることを示した．そこでは伝導電子の有効質量m*は発散し，Fermi面における電子の分布関数nkFの不連続は消える．Mott絶縁体ではAndersonの超交換相互作用が働くので，これは金属から局在反強磁性への転移である．しかし，Gutzwiller理論ではスピンの反強磁性相関は排除されているから，正しくは金属側においても反強磁性相関を考慮に入れなければならない．このときは金属-絶縁体転移はBrinkman-Riceほど単純なものにはならないであろう．これがBrinkman-Riceに対する第1の疑問点である．第2にはGutzwiller近似は何といっても大雑把過ぎる．さらにはGutzwillerの変分関数そのものに対する疑問がある．32)

Brinkman-Rice以後，このGutzwiller近似をめぐっていろいろの検討が加えられた．Metzner-Vollhardt33) (1988)は1次元系でエネルギー期待値を厳密に計算した．その結果によると，1次元ではMott転移は起こらない．このことは横山-斯波32)の結論とも一致している．したがってGutzwiller近似は正しくない．しかし，次元が無限大の場合，Gutzwiller近似は厳密に成立し，ここではBrinkman-Riceは正しいことになる．

1次元Hubbard模型に対しては，Lieb-Wu34)(1968)によって厳密解が得られた．1次元厳密解の研究は最近，小形-斯波，35)川上-梁36) (1990)などによってさらに詳細に進められた．それによると，n＝1のhalf-filledの場合は，Lieb-Wuによって示されたように，U 0である限り常に絶縁体であって，U ＝0は特異点になっている．しかし，n 1のときはFermi液体ではなく，Luttinger液体になっている．Luttinger液体ではFermi面における電子の分布関数nkFには不連続はなく，

　

のように振舞う．qはn 〜1の場合，1/8に近い臨界指数である．

高温超伝導に関連して，2次元Hubbard模型の場合が問題になっている．Andersonは2次元においてもLuttinger液体になっていると主張しているが，2次元ではFermi液体状態が成立していて，Fermi面の分布に不連続が残っているという主張もある．現在のところ明確な決着には到っていないようである．

また，最近では無限次元Hubbard模型の研究が盛んに行われている．ここではGutzwillerの変分法によらず，Mott転移が起こることがRozenberg37)らによって示され，Mott転移近傍の様子がより詳しく調べられている．ただし，これが3次元系にも成立するかどうかは難しい問題である．

ここで，3d金属強磁性の問題に戻り，金森らの強相関の理論以後に展開された守谷理論について言及する．守谷-川畑38, 39)(1973)はSCR(self-consistent renormalization)と名づける近似法に基づき，強磁性，反強磁性金属の特に転移点以上の磁性の研究を行った．この近似は本質的にはRPA (random phase approximation)で記述されるスピンのゆらぎのmode間にmode-mode結合を導入し，全体を自己無憧着に解を求めるというものである．守谷はこの近似理論によってSlater-Stonerの困難がすべて除去され，実験結果をよく再現する結果がえられることを示した．守谷理論は最初，弱い強磁性，反強磁性体を対象に展開されたが，後に強相関の場合にも拡張され，この近似理論によってMott転移の問題を議論した．

高温超伝導体，特にunderdopedの領域は伝導電子数がhalf-filledに近く，強相関をもつ金属状態にあると考えられる．この意味からも，Mott転移の近傍にある金属電子の問題は現在の重要課題であって，現に活発な研究が進行しているところである．

§6.　近藤効果と重いFermi粒子

近藤効果についての最初の論文40)が発表されたのは1964年である．それからこの問題はWilson41) (1974)の繰り込み群に基づく理論展開，山田-芳田42, 43)(1975)のAnderson模型に立つFermi液体理論を経て，興地-川上44)(1981)によるAnderson模型の厳密解に至り，一応の区切りがつけられた．この間，近藤効果について多くの研究がなされてきた．また，近藤効果に付随して重要な理論展開があった．その一つはAnderson44)(1967)の直交定理の証明である．いま，球対称の不純物ポテンシャルを考える．このポテンシャルによって伝導電子は散乱を受ける．このとき，散乱を受けた電子系の基底状態の波動関数 jfと不純物ポテンシャルのない場合の基底状態 ji との重なり積分は次の形で互いに直交する．特にs波散乱の場合を考えると，
　

が成立する．ここに，d(eF)は散乱されたs波の位相シフトのFermiエネルギーでの値であり，Nsはs波の電子数である．d(eF)0に対して(12)式はNs→∞で消える．これがAndersonの直交定理である．初めの状態jiにも不純物ポテンシャルが作用し，その位相シフトをdi(eF)とすれば，このときの重なり積分は(12)式のd(eF)をdf(eF)-di(eF)で置き換えることにより得られる．d/pはFriedelの和則(8)式によれば，不純物原子の廻りに局在した電子数である．従って，Andersonの直交定理は局在電子数が異る二つの基底状態の波動関数が直交することを意味する．見方を変えると，この定理は局在電子数の保存を意味するとも考えることができる．Andersonの直交定理はFriedelの和則とともに，金属電子論における重要な定理であって，多くの問題に適用することができる．

Andersonの直交定理のほか，もう一つの重要な研究は，Mahan46)(1967)及びNozires-de Dominicis47) (1969)による軟X線の異常吸収端及び異常放射端の理論である．金属の軟X線の異常端の問題は随分古くから知られていたにも拘わらず，長く未解決のままであった．それが，この理論によって見事に解決されたのである．

近藤効果とは要するに，非磁性金属中の磁性不純物の局在スピンが温度低下とともに，反強磁性的交換相互作用によって誘起された伝導電子の逆向きのスピン偏極によって打ち消され，T ＝0で完全にそのスピンを消失する現象である．絶対零度では局在スピンは伝導電子のスピン偏極と結合してスピン1重項を形成するため，局在スピンは存在しない．温度が上昇すると局所的にスピンの揺らぎが発生する．局在スピンはこの揺らぎが成長したものである．

近藤効果は，前に述べたように，局在スピン間のRKKY相互作用が無視できるような稀薄合金で観測される一つの不純物原子の局在スピンに関する現象である．しかし，稀土類，特にCeの金属間化合物CeAl2, CeAl3, CeCu2Si2などでは，磁性イオンである稀土類イオンは各格子点に存在しているにも拘わらず，高温側で近藤効果が観測される．電気抵抗は温度低下とともに-log(T /D )に比例して増大する．この現象は高密度近藤効果とよばれる．高密度近藤効果は近藤効果を特徴づける温度TKが異常に大きく，RKKY相互作用に打ち勝っているために起こると考えられる．TKが異常に大きいのは4f軌道の縮退によることが指摘されている．

高密度近藤状態は，低温では有効質量の異常に大きい正常の金属電子の状態に移る．この状態は重いFermi粒子と呼ばれる．高密度近藤状態は局在スピンの自由度のために大きなエントロピーをもつから高温で安定である．低温では4f軌道は伝導電子の軌道とのmixingによってコヒーレントな遍歴電子となり，エントロピーの小さい状態に移る．この遍歴4f電子のコヒーレンスは温度によって，あるいは磁場によって破れ，高温，強磁場下では高密度近藤状態に移行する．このような稀土類金属化合物では各格子に4f電子軌道を置いたAnderson模型，すなわち周期的Anderson模型が適当なモデル・ハミルトニアンと考えられる．重いFermi粒子系の特性は，この模型に立つFermi液体理論によってその大綱は理解できる．この方向の理論展開については，山田耕作48)による著書『電子相関』第7章に要を得た解説がなされているので，それを見ていただくことにして，ここでは立ち入らない．

稀土類を含む金属間化合物は，鉄族金属とは異った複雑で豊富な物性を示す一つの大きな物質群を形成する．高密度近藤状態や重いFermi粒子の形成などは，その顕著な特性の例である．我が国におけるこのような稀土類化合物の研究の伝統を作ったのは東北大学の糟谷を中心とするグループであり，彼らは早くからこの物質群の示す豊富な物性に着眼し，その試料作成から物性の研究に幅広い努力を重ねてきた．現在の磁性研究の重要課題は，まだまだ多くの未解決の問題を内蔵しているこのような稀土類化合物，あるいは5f電子を含むウラン化合物における磁性，超伝導などの物性の研究である．将来の大きな研究の進展が期待される．

文　献

  1. L. Nel: Ann. Phys. (France) 3 (1948) 137.
  2. C.G. Shull and J. S. Smart: Phys. Rev. 76 (1949) 1256.
  3. P.W. Anderson: Phys. Rev. 79 (1950) 350.
  4. P.W. Anderson: Phys. Rev. 115 (1959) 2.
  5. N. Bloembergen, E.M. Purcell and R.V. Pound: Phys. Rev. 73 (1948) 679.
  6. P.W. Anderson and P. R. Weiss: Rev. Mod. Phys. 25 (1953) 265.
  7. R. Kubo and K. Tomita: J. Phys. Soc. Jpn. 9 (1954) 888.
  8. P.W. Anderson: Phys. Rev. 86 (1952) 694.
  9. R. Kubo: Phys. Rev. 87 (1952) 568.
  10. C. Zener: Phys. Rev. 81 (1951) 440.
  11. M.A. Ruderman and C. Kittel: Phys. Rev. 96 (1954) 99.
  12. T. Kasuya: Prog. Theor. Phys. 16 (1956) 45.
  13. M.K. Wilkinson, W.C. Koehler, E.O. Wollan and J.W. Cable: J. Appl. Phys. 32 (1961) 20S, 48S, 49S.
  14. A. Yoshimori: J. Phys. Soc. Jpn. 14 (1959) 807.
  15. P.W. Anderson: Phys. Rev. 124 (1961) 41.
  16. J. Friedel: Nuovo Cimento Suppl. 2 (1958) 287.
  17. J. Bardeen, L.N. Cooper and J. R. Schrieffer: Phys. Rev. 108 (1957) 1175.
  18. V.L. Ginzburg and L.D. Landau: Zh. Eksp. Teor. Fiz. 20 (1950) 1064.
  19. A.A. Abrikosov: Sov. Phys.-JETP 5 (1957) 1174.
  20. R. Kubo: J. Phys. Soc. Jpn. 12 (1957) 570.
  21. L.D. Landau: Sov. Phys.-JETP 3 (1957) 920, 5 (1957) 101, 8 (1959) 70.
  22. J.M. Luttinger: Phys. Rev. 119 (1960) 1153.
  23. P. Nozires: Theory of Interacting Fermi Systems (Benjamin, 1964).
  24. A.A. Abrikosov, L.P. Gorkov and E. Dzyaloshinski: Methods of Quantum Field Theory in Statistical Physics (Prentice-Hall, 1963).
  25. T. Matsubara: Prog. Theor. Phys. 14 (1955) 351.
  26. P.W. Anderson: Phys. Rev. 109 (1958) 1492.
  27. E. Abraham, P.W. Anderson, D.C. Licciardero and T.V. Ramakrishnan: Phys. Rev. Lett. 42 (1979) 673.
  28. J. Hubbard: Proc. R. Soc (London) A 276 (1963) 238, 277 (1964) 237.
  29. J. Kanamori: Prog. Theor. Phys. 30 (1963) 275.
  30. M.C. Gutzwiller: Phys. Rev. Lett. 10 (1963) 159; Phys. Rev. 134 (1964) A923, 137 (1965) A1726.
  31. W.F. Brinkman and T.M. Rice: Phys. Rev. B 2 (1970) 4302.
  32. H. Yokoyama and H. Shiba: J. Phys. Soc. Jpn. 59 (1990) 3669.
  33. W. Metzner and D. Vollhardt: Phys Rev. Lett. 59 (1987) 121, 62 (1989) 324; Phys. Rev. B 37 (1988) 7382.
  34. E. Lieb and F.Y. Wu: Phys. Rev. Lett. 20 (1968) 1446.
  35. M. Ogata and H. Shiba: Phys. Rev. B 4 (1990) 2326.
  36. N. Kawakami and S.-K. Yang: Phys. Rev. Lett. 65 (1990) 2039.
  37. M.J. Rozenberg, X.Y. Zhang and G. Kotliar: Phys. Rev. Lett. 69 (1992) 1236, 70 (1993) 1666.
  38. T. Moriya and A. Kawabata: J. Phys. Soc. Jpn. 34 (1973) 639, 669.
  39. T. Moriya: Spin Fluctuations in Itinerant Electron Magnetism (Springer-Verlag, 1985).
  40. J. Kondo: Prog. Theor. Phys. 32 (1964) 37.
  41. K. Wilson: Rev. Mod. Phys. 47 (1975) 773.
  42. K. Yamada: Prog. Theor. Phys. 53 (1975) 970, 54 (1975) 316.
  43. K. Yosida and K. Yamada: Prog. Theor. Phys. 53 (1975) 1286.
  44. N. Kawakami and A. Okiji: Phys. Lett. 86A (1981) 483. A. Okiji and N. Kawakami: J. Appl. Phys. 55 (1984) 1931.
  45. P.W. Anderson: Phys. Rev. Lett. 18 (1967) 1049; Phys. Rev. 164 (1967) 352.
  46. G.D. Mahan: Phys. Rev. 163 (1967) 612.
  47. P. Nozires and C. T. de Dominicis: Phys. Rev. 178 (1969) 1097.
  48. 山田耕作：『電子相関，現代物理学16』（岩波書店，1993）．