|
|
| 50年をかえりみる |
Anderson局在の研究--弱局在からメゾスコピック物理へ--
長岡洋介
〈京都大学基礎物理学研究所 606-01京都市左京区北白川追分町〉
1. スケーリング理論まで
この50年の固体電子論の発展をみると,1950年代後半から60年代の初めにかけていくつかのピークが現れ,そこからの研究の流れが現在に続いていることに気づく.第一に挙げるべきピークは,なんといっても超伝導のBCS理論(1957年)1)だろう.さらに,不規則ポテンシャル中の電子状態の局在を論じたAndersonの理論(1958年)2)があり,抵抗極小の近藤論文(1964年)3)が出ている.固体電子論の研究にかかわってきた人たちは,誰もがどこかでこの研究の流れに多少なりと関係をもってきたといってよい.
超伝導と近藤効果の研究が50〜60年代から今日まで,絶え間なく発展してきたのに比べると,Anderson局在の研究は少し様子が違っている.Andersonの後,MottやThoulessの研究が続いたものの,不規則性の取扱いの難しさが長く研究の大きな発展を拒んできたのである.実験では,Anderson以前に佐々木亘らによる半導体の不純物伝導における負の磁気抵抗の発見(1956年)4)という重要な寄与があるが,これがAnderson局在の効果だとわかるのはずっと後のことだ.
このような状況に突破口を開いたのはAbrahamsらによるスケーリング理論(1979年)5)であった.この理論の意義は,局在を正面から問題にするのではなく,試料のコンダクタンスの試料サイズ依存性をみるという新しい視点を導入したところにあった.局在した電子の波動関数の広がりξが原子スケールより十分に大きいとすれば,試料サイズLがL≪xのとき試料には電流が流れ,コンダクタンスは普通の金属と同じように振舞うだろう.一方L≫xで試料は絶縁体になる.その間がどうつながるかをスケーリングの考え方で考察するのがこの理論である.
スケーリング理論から得られた結論はつぎのようなものであった.
(1) 3次元では,不規則ポテンシャルを強くしていくと金属状態から絶縁体へ(2次の)転移が起こる.
(2) 1, 2次元では,電子状態は不規則ポテンシャルの強さにかかわりなく,つねに局在する.
(3) 2次元では,試料サイズLが大きくなると,伝導率sにlog Lに比例する項が現れる.すなわち
![]()
ここで,s0はDrudeの式で与えられる普通の金属の伝導率
![]()
である.m, e は電子の質量と電荷,n は電子密度,tは緩和時間である.
この結果で注目すべきことの一つは,試料サイズを大きくしていくと,試料が局在によって絶縁体になる前に,局在の前触れ的な現象がみられることだ.2次元でいえば,式(1)の第2項がそれである.この前触れをみるだけであれば,そこでは不規則ポテンシャルの効果はまだ弱いのだから,不規則ポテンシャルを摂動として扱うことも許されるだろう.このような視点にたった次のステップが,Gorkov, Larkin, Khmelnitzkyの理論(1979年)6)であった.
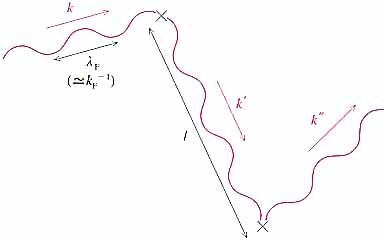
電気伝導率の計算は通常Boltzmann方程式によってなされ,Boltzmann方程式からDrudeの式(2)を得るのは容易である.しかし,Boltzmann方程式では,いろいろな波数の状態にある電子が別の波数の状態に散乱される,という見方がなされているから,図1のように電子の平均自由行程lは波長に比べて十分長くなければならない.金属の場合,Fermi波数をkFとすれば,条件は
![]()
である.この条件が満たされなくなると,式(2)に対して(kFl)−1のオーダーの補正がつくに違いない.2次元ではn〜k2Fだから,l=vFt(vFはFermi速度)として補正項の大きさは
![]()
と見積られる.式(1)の第2項はこのオーダーの量になると考えられる.
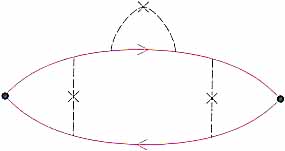
補正はBoltzmann方程式を超える量子補正として現れるのだから,その計算は久保公式から出発しなければならない.不純物散乱による伝導率を久保公式から求めるには,不純物ポテンシャルを摂動として摂動展開を行う.各不純物による散乱が独立に起こるとする近似で,摂動項を無限次まで加えあわせることにより,Drudeの式(2)を導くことができる.摂動項を表すグラフの一例が図2である.
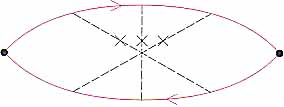
補正項を求めるには,この近似を超える計算をしなければならない.Gorkovらはそれが図3のようなグラフで与えられることを示した.この図は3個の不純物による3次の散乱過程を表している.彼らはこのような項がとくに低次元では大きな寄与を与えることを見出し,これを無限次まで加えあわせることにより,2次元では
![]()
を得た.結果はスケーリング理論の予想と一致し,ここでは係数まで決まったことになる.
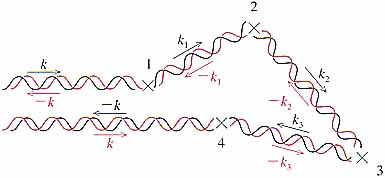
この効果は物理的にはつぎのように理解できる.電子の波が不純物の分布する試料に入射したとしよう.この波が図4のように何個かの不純物とつぎつぎに相互作用し,真後ろに散乱される場合を考える.散乱には時間をちょうど逆にした過程もある.ここで注意すべきことは,不純物によるポテンシャルは空間的には不規則だが,時間反転に対しては対称であることだ.このため,二つの過程による後方への散乱波はちょうど同位相になるのである.同位相の二つの波は干渉して強めあい,後方散乱の確率が増大する.これが伝導率の減少をもたらすのだ.後方散乱が量子補正の因であるとすれば,全散乱確率への後方散乱の寄与がどれだけかを考えて,効果が低次元ほど重要になることは明らかだろう.局在の前駆現象として現れるこの効果は弱局在効果とよばれる.
理論と実験を比べるには,もう一歩の考察が必要である.上の結果は有限の大きさLをもつ試料について,絶対0度で求めたものだ.実験はマクロな試料,つまりLの十分に大きな系について,有限の温度で行われる.有限温度では,電子はフォノンや他の電子と非弾性散乱を起こし,波動関数の位相が乱されるから,電子波が干渉しうる広がりはそれによって制限される.その長さをLeとすれば,マクロな系は長さLeの部分系に分けられ,各部分系ごとに式(5)の伝導率の補正が生じると見てよい.したがって,有限温度のマクロな系における補正は,式(5)でL=Leとおいたものになる.Leは,不純物に衝突しながら拡散的に運動する電子が非弾性散乱の緩和時間teの間に移動する距離としてよいから,拡散係数をDとして,
![]()
と見積ることができる.ここで,teは絶対0度で無限大になるから,
![]()
とおくと,
![]()
となり,伝導率に対数的な温度依存性が現れる.
この2編の短い論文がその後のAnderson局在研究の爆発的な発展に火をつけたのだが,残念ながらここまではわが国における研究の寄与はない.もちろん,Gorkovらの研究で基本的な役割をしている久保公式は別にして,の話である.これに続くわが国における研究の開始には二つのきっかけがあった.一つは第2の論文の著者の1人,Larkinの来日であり,もう一つはAndersonのいたBell研究所を訪問した久保亮五の土産話だった.
|
|
図1 不純物による電子の錯乱(Boltzmann方程式の描像) |
 |
|
図2 伝導率のグラフ.Drudeの式を与える. |
 |
|
図3 伝導率のグラフ.両氏補正を与える. |
 |
2. 弱局在事始
1979年9月3日から6日まで,山中湖畔のホテルで第2回2次元電子系国際会議があり,これに引き続いて8日から12日まで基礎物理学研究所で第2回京都サマーインスティチュート「低次元の物理」が開かれた.この会議に国外からの招待講演者としては Emery, Halperin, Sham らが出席している.最初の予定ではここにLarkinも出るはずであった.それが手違いで会議に間にあわなかったのである.
Larkinの招へいは,すでに学術振興会からの援助が決まっていたので,結局1カ月遅れで実現した.彼は10月6日から約1カ月間基研に滞在している.この間に書かれたのが,氷上,Larkin,長岡の論文(1980年)7)である.
来日したとき,LarkinはすでにGorkovらの理論を磁場のある場合に拡張した結果を得ていた.その理論は上記論文より少し遅れて発表されている.8)基研で氷上らと共同でなされたのは,スピン軌道相互作用がある場合の計算である.
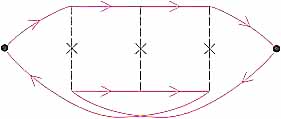
図3のグラフは少し書きなおすと図5のようになる.こうすると,グラフの中心部分は多体問題でしばしば遭遇する「はしご型」になる.超伝導でCooper対が出て来るグラフも同じ型のものであり,磁場がある場合の計算もなされている.ここではそれを応用すればよかった.
すでに述べたように,伝導率の量子補正は不純物ポテンシャルが時間反転の対称性をもつことによる後方散乱の増大がその因であった.磁場が加わると時間反転の対称性が破れる.したがって,磁場は局在の効果を弱め,量子補正を減らす働きをする.磁場によって抵抗の増大が減るから,負の磁気抵抗が現れるのだ.
では,スピン軌道相互作用があると何が起こるか.結果は意外であった.量子補正の符号が逆になったのである.これは,スピン軌道相互作用が強いと,電子波の干渉によって後方散乱が弱められることを意味していた.
不純物が普通のポテンシャル散乱だけをする場合,磁場がある場合,スピン軌道相互作用が強い場合.この三つの場合,電子のハミルトニアンのもつ対称性が異なっているのである.その違いが原子核や金属微粒子における準位の分布に現れることは,ランダム行列の理論によってすでにわかっていた.それが局在効果の現れ方にも基本的な違いをもたらすのである.氷上らの理論はそのことを明らかにしたのであった.氷上はこの後,この対称性の違いに着目して,くりこみ群の方法に基づく理論を展開している.
じつは,高次の不純物散乱が電子の非弾性散乱によって抑制され,このため温度が上がると抵抗が減少するという考え方は,ずっと以前に現れている.それは横田紀男の理論(1958年)9)である.私はこの話を久保研究室のコロキウムで聞いた.横田の理論は抵抗極小を説明することを目的としていたが,もちろんそのためのものとしては成功していない.計算も2個の不純物による散乱までしかなされていなかった.しかし,考え方自身は弱局在効果の理論と基本的に同じであり,きわめて優れたアイデアであったと思う.
|
|
図5 伝導率のグラフ.(図3)の書きなおし. |
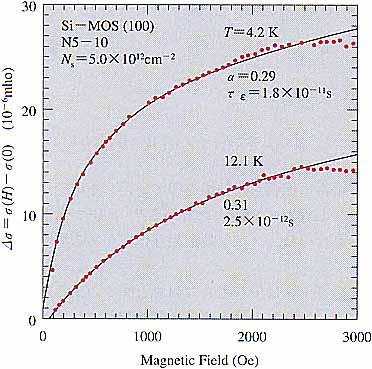 |
| 図6 MOS 2次元電子系の磁気抵抗(Y.Kawaguchi and S.Kawaji: J. Phys. Soc. Jpn. 48 (1980) 699より転載.) |
3. 半導体界面2次元電子系の実験
私がLarkinから負の磁気抵抗の話を開いたとき,すぐ心に浮かんだのは川路紳治らの実験のことであった.川路らは1960年代から半導体界面に形成される2次元電子系の研究を続けており,数々の成果を挙げていた.その中で,通常の磁気抵抗の現れる磁場よりはるかに弱磁場で,負の磁気抵抗が現れるのを発見していたのである.この実験結果は1978年に発表されていたが,10)私はそれは読んでいない.Larkin来日の直前,愛媛大学で開かれた物理学会分科会におけるシンポジウム「半導体における異常な磁気抵抗」で,川口洋一の講演「MOS反転層の負磁気抵抗」を聞いていたのである.抵抗の変化は磁場の2次元面に垂直な成分に依存しており,効果が電子の軌道運動に対する磁場の影響によるものであることを示していた.
私は川路に電話をして実験データを送ってもらった.抵抗変化の大きさなどを当ってみると,理論の結果とほぼ一致していた.詳しくいうと若干の違いはあるのだが,川路らの実験が局在効果を示していることは間違いないと確信した.
Larkinは基研滞在を終えて帰国の途中,東京へ立ち寄り,学習院大学を訪問した.ここで川路らとさらに議論を行っている.Larkinから理論の結果を得て,川口と川路は理論と実験の詳しい比較を試る.その結果が図6である.11)ここでは全体にかかる係数と電子の非弾性散乱による緩和時間teをパラメーターとして合わせているが,磁場依存性の傾向は見事に一致している.
係数の不一致は,MOS反転層の電子系の特殊事情によるものであることが,少し後に福山秀敏によって示された.12)シリコンの伝導帯には,エネルギー最小の点(谷)が4個存在する.これを(1, 0, 0)面で切ってできた2次元電子系では,谷は2個になる.もしもこの二つの谷にある電子間にまったく往き来がないとすれば,二つの谷を占める電子系は独立に振舞うわけで,量子補正はそれぞれから式(5)の分だけ現れ,全体としては2倍になる.他方,谷間の往来が頻繁になされているなら,電子全体が一つの電子系として振舞い,量子補正は式(5)のままである.電子の谷間散乱の具合いによっては,係数は2と1の中間になりうるのである.これが,パラメーターとしてとられた係数の意味であった.
ここで注目すべきことは,この理論と実験の比較によって,単に実験的に見出された負の磁気抵抗の原因が明らかになっただけでなく,このほかの方法では知りえない電子系の性質が明らかになったことである.その一つは,非弾性散乱による緩和時間teである.
|
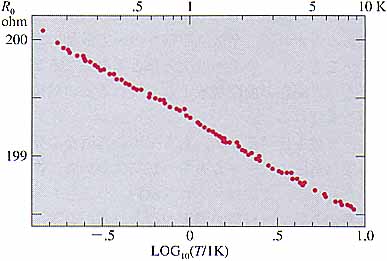
| 図7 Cu膜の抵抗の温度依存性.(S.Kobayashi, et al.: J. Phys. Soc. Jpn. 49 (1980) 1635より転載.) |
4. 金属薄膜2次元電子系の実験
川路らの半導体界面2次元電子系の実験と並んで,局在効果の研究で大きな成果を挙げたのは,小林俊一らの金属薄膜の実験であった.
小林の回想によると,事の起こりはBell研究所を訪問して帰国した久保亮五との廊下での立話だった.小林君,2次元では抵抗にlog Tが出るというおかしな話があるんだがネ--といった話だったらしい.小林らは孤立した金属微粒子による久保効果の研究をしており,次には微粒子を集めて個々の微粒子に孤立した電子がどのように動き出すかを見たい,と考えていたところだった.早速,微粒子を2次元的に並べて,実験にとりかかることにした.
小林が酸化微粒子膜とよぶこの試料はなかなか独得なものだ.真空蒸発で金属微粒子をつくり,薄く板の上に受ける.これを短時間空気にさらして微粒子の表面を酸化させる.このプロセスをくり返すことによって,表面が酸化した金属微粒子の堆積した2次元膜をつくるのである.この試料の特徴は,酸化時間を加減することで抵抗値の異なる試料を自在につくることができる点にある.
さて,こうしてできた銅の薄膜による実験結果は図7のようで,見事に対数的な温度依存性を示した.13)金属薄膜でlog Tを見る実験としてはDolanとOsheroff14)に先を越されたが,温度の2桁にわたる範囲でlog Tが見えているデータの見事さはDolanたちをしのいでいる.小林たちはこの後,磁気抵抗,局在効果の膜の厚さ依在性(2次元から3次元へのクロスオーバー)など,さまざまな実験を精力的に行っている.外国ではBergmanが小林たちより一歩遅れて金属薄膜の実験を始めた.
|
|
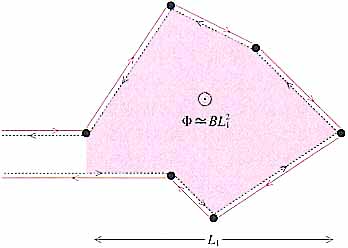
図8 磁場による電子派干渉効果の抑制. |
5. 3次元の弱局在,相互作用の効果
最初の氷上らの仕事に続く理論の成果は,3次元系における局在効果の問題と電子間相互作用の効果の発見であった.
3次元における局在効果を論じたのは川畑有郷である.15)スケーリング理論によると,有限系の伝導率には試料が金属的に振舞う領域においても,試料サイズLに反比例する量子補正が現れる.すでに述べたように,有限温度ではLが電子波の干渉が可能な長さLe(式(6))に置きかわる.磁場が加わると,この量子補正が抑えられて負の磁気抵抗が現れるのである.ごくおおまかには,磁場によって干渉性の壊される長さLBが,LB<LeではLeに置きかわると考えてよい.
LBは次のような考え方で見積ることができる.電子波が図8のように,ある広がりL1の領域にある不純物によって後方へ散乱されるとしよう.これと時間反転の関係にある過程を経る散乱を比べると,磁束密度Bがあるときには,散乱の道すじが囲む磁束をF (〜BL12)とすれば,二つの散乱波の間に
![]()
の程度の位相差が生じる.ただし,f0は磁束量子h/eである.これは一種のAharonov-Bohm効果である.この位相差が1のオーダーになれば,電子波の干渉は著しく損われるだろう.したがって,LBは
![]()
としてよい.結局,磁場による抵抗の減少はLB<Leのとき,![]() に反比例することになる.もちろん,定量的な結果を得るには,摂動論によるきちんとした計算をしなければならない.
に反比例することになる.もちろん,定量的な結果を得るには,摂動論によるきちんとした計算をしなければならない.
ここでも理論と実験の一致は見事であった.こうして,半導体の不純物伝導における負の磁気抵抗の謎は,発見から四半世紀を経て解かれたのである.
もちろん,川畑の理論の前にも,謎を解こうとする理論の試みは存在した.その中で私が記憶しているのは豊沢 豊の理論である.16)豊沢は負の磁気抵抗は磁性不純物によるものと考えた.磁性不純物による電子の散乱が電気抵抗に寄与している場合には,磁場を加えると不純物のスピンが揃うことによって不規則さが減り,抵抗も減少する.このことは希薄合金の場合についてはすでに知られていた.半導体の不純物伝導では,不純物はランダムに分布しているから,中には孤立気味の不純物もあって,それらの不純物が希薄合金のときのAnderson模型のように磁性不純物となって,負の磁気抵抗の因になる--というのが理論の筋書きであった.その頃,私自身が磁性不純物の問題に興味をもっていたこともあって,この理論は私にはたいへん魅力的であった.ここにAnderson局在の考え方はないが,局在と電子相関との相乗効果の可能性を明らかにした優れたアイディアであった.
電子間相互作用の効果に関する理論は福山によるものである.17)電子の波動関係が局在する傾向を示すと,それが電子間相互作用にも影響し,ひいては電気伝導率にも寄与する.そこにはいろいろな過程からの寄与があり,ひと口で単純な物理的説明を加えることは難しいが,結果としては,2次元系の伝導率に関しては,局在効果のみの場合と同じ温度依存性(log T)をもつ,同じオーダーの寄与が現れるのである.したがって,実験の解析も単純な局在効果の理論のみではなしえないことになる.Fermi液体論によると,不規則さのない系では電子間相互作用はFermi面近傍の電子の性質に大きく影響することはない.不規則な系では事情が違うのである.このことは,はじめAltshulerとAronov18)によって見出されたが,スケーリング理論の前であったこともあって,分析は十分にされていない.相互作用の効果は福山と独立にAltshuler, Aronov, Lee19)によっても論じられている.
6. 研究の発展
このように,国内での研究が一斉に始まったので,一度集って議論しようと,基研で研究会を開いたのは1980年の5月であった.私の手帳によると,参加したのは川畑,福山,川路,川口のほか芳田奎,それに基研の氷上と私である.小規模ではあるが,これがこのテーマで開かれた最初の研究会であった.
翌1981年には谷口シンポジウムにAnderson局在がとり上げられた.20)谷口シンポジウムの本来の趣旨は,重要な,しかしあまり注目されていないテーマをとり上げ,若手を中心に小規模な国際シンポジウムを開くのを援助するもの,この趣旨に合わないのではないか--といった意見を谷口シンポジウムの委員であった久保先生からいただいた記憶がある.会議の準備が始まった80年の秋頃には,それだけこの問題は世界中で注目されていたのである.会議は11月の3日から8日まで,三田市にある関西学院大学のセミナーハウスで開かれ,国外からはThouless,Wegner,Lee, Imry, W![]() lfle, Toulouse, MacKinnonが,国内からはすでに名前の出た氷上,川畑,福山のほか,久保,上村,米沢,安藤ら15名が参加した.Andersonも出席の予定であったが,会議の直前に病気になり,出席がとり消されている.
lfle, Toulouse, MacKinnonが,国内からはすでに名前の出た氷上,川畑,福山のほか,久保,上村,米沢,安藤ら15名が参加した.Andersonも出席の予定であったが,会議の直前に病気になり,出席がとり消されている.
1981年からは佐々木亘が代表者になって科研費の総合研究が発足している.これは,翌年から特定研究「超低温にいたる量子凝縮相の研究」にひき継がれ,研究の発展に大きな役割を果した.
1985年,プログレスのサプリメントとして“Anderson Localization"が出版された.21)この号には,すでに述べた氷上,川畑,福山らの理論,川路,小林らの実験のほか,量子Hall効果の理論(安藤,吉岡ら)と実験(吉広ら)の報告も掲載されている.要するに,この時期までのわが国における研究の集大成であった.そして,それがそのままこの分野における研究の優れたレビューになっているところに,わが国における研究のレベルの高さが示されている.
1987年には第18回低温物理国際会議が京都で開催され,そのサテライトとして“Anderson Localization"の会議が東大シンポジウムとして東大山上会館で開かれた.22)高温超伝導で湧いたLT18に比べると注目度は低かったが,内容的にはきわめて稔り豊かな会議であった.ここでは,弱局在効果の問題だけでなく,3次元における金属絶縁体転移に関しても優れた研究が発表されている.その中でとくに勝本信吾の研究に触れておきたい.
金属絶縁体転移では,電子密度,不純物濃度などの試料を特徴づけるパラメーターを連続的に変化させたとき,コンダクタンスが転移点でどのようなパラメーター依存性を示すかが問題になる.これを実験的に確かめようとすると,例えば不純物濃度の異なる試料を多数用意しなければならない.しかし,試料の数にも限りがあるから,転移点近傍での振舞を正確に知ることはきわめて難しい.勝本は試料として永久光伝導体を用いることによって,この困難を克服した.ある種の半導体では光伝導の減衰時間がきわめて長く,事実上それは永久に持続するとみてよい.このような物質(実際に用いたのはAlGaAs: Si)を試料に用いると,光を当てる時間を連続的に変えることにより,キャリア濃度を連続的に変えることができるわけである.勝本はこのような方法によって,キャリア濃度nを変化させると伝導率は転移点(nc)の近傍において(n−nc)に比例して連続的に0になることを示した.
この会議のもう一つの特徴は,メゾスコピック系の問題がとり上げられたことである.Anderson局在は電子波の干渉がその本質であった.それは,固体における電子波の量子干渉効果を見る--という点で,固体物理に新しい分野を切り開くものであった.弱局在効果では,その干渉が温度や磁場によって妨げられる様子を,コンダクタンスの変化として見ている.もしも温度が十分に低く,試料が十分に小さければ,干渉効果そのものが見えてくるだろう.Anderson局在の研究はこうして自然にメゾスコピック系の研究へとつながったのである.
Anderson局在からメゾスコピック系への研究の発展は,固体における電子波干渉効果の研究という新しい分野を切り開くものであった.この新分野は,きわめて基礎的な問題が高度な新技術やデバイスにもつながる工学的な問題と密接に関連する点でも注目される.その初期の段階で,わが国の研究者たちがきわめて重要な寄与をなしたのであった.技術的にも高い水準にあるわが国が,この分野で今後も同様な役割を果すことを期待したい.
参考文献
- J. Bardeen, L. N. Cooper and J. R. Schrieffer: Phys. Rev. 108 (1957) 1175.
- P. W. Anderson: Phys. Rev. 109 (1958) 1492.
- J. Kondo: Prog. Theor. Phys. 32 (1964) 37.
- W. Sasaki and Y. Kanai: J. Shys. Soc. Jpn. 11 (1956) 894.
- E.Abrahams,P.W.Anderson,D.C.LicciardelloandT.V.Ramakrishnan:Phys. Rev. Lett. 42 (1979) 673.
- L. P. Gorkov, A. I. Larkin and D. E. Khmelnitzkii: Pis'ma Zh. Eksp. Teor. Fiz. 30 (1979) 248 [JETP Lett. 30 (1979) 228].
- S. Hikami, A. I. Larkin and Y. Nagaoka: Prog. Theor. Phys. 63 (1980) 707.
- B. I. Altshuler, D. E. Khmelnitzkii, A. I. Larkin and P. A. Lee: Phys. Rev. B 22 (1980) 5142.
- 横田紀男:物性論研究2集 4 (1958) 239.
- Y. Kawaguchi, Y. Kitahara and S. Kawaji: Surf. Sci. 73 (1978) 520.
- Y. Kawaguchi and S. Kawaji: J. Phys. Soc. Jpn. 48 (1980) 699.
- H. Fukuyama: J. Phys. Soc. Jpn. 49 (1980) 649.
- S. Kobayashi, F. Komori, Y. Ootuka and W. Sasaki: J. Phys. Soc. Jpn. 49 (1980) 1635.
- G. J. Dolan and D. D. Osheroff: Phys. Rev. Lett. 43 (1979) 721.
- A. Kawabata: Solid State Commun. 34 (1980) 432; J. Phys, Soc. Jpn. 49 (1980) 628.
- Y. Toyozawa: J. Phys. Soc. Jpn. 17 (1962) 986.
- H. Fukuyama: J. Phys. Soc. Jpn. 48 (1980) 2169.
- B. L. Altshuler and A. G. Aronov: Solid State Commun. 30 (1979) 115.
- B. L. Altshuler, B. L. Aronov and P. A. Lee: Phys. Rev. Lett. 44 (1980) 1288.
- Y. Nagaoka and H. Fukuyama, ed.: Anderson Localization, Springer Series in Solid-State Sciences 39 (Springer, 1982).
- Y. Nagaoka, ed.: Anderson Localization, Prog. Theor. Phys. Suppl. No. 84 (1985).
- T. Ando and H. Fukuyama, ed.: Anderson Localization, Springer Proceedings in Physics 28 (Springer, 1987).