|
|
| 50年をかえりみる |
線形応答理論の成立
中嶋貞雄
〈超電導工学研究所 135東京都江東区東雲1-10-13〉
1. 序論
辞典スタイルの堅い話から始めて恐縮だが,統計力学の対象となるマクロな力学系は,熱平衡系と非平衡系に大別され,後者はさらに,熱平衡からの外れを1次の微少量とみなしてよい線形非平衡系と,この近似の許されない非線形非平衡系とに大別される.本稿の対象は,線形非平衡系の統計力学である.
オームの法則に従って電流の流れている導体が線形非平衡系の身近な実例だが,この種の系を扱う場合の理論スキームとして,熱平衡系の統計力学に劣らない一般性を具えた線形応答理論 (linear response theory) がある.マクロな力学系に外場(例えば交流電場)を加えて熱平衡を攪乱したとして,攪乱に対し系の示す応答(例えば系に流れるマクロな電流)を外場の1次のオーダーで考えるのである.応答はもちろん外場の強さに比例し,比例係数が輸送係数(例えば電気伝導度)をあたえることになる.こうして,輸送係数を系の力学変数で表す公式(いわゆる Kubo formula)が導かれ,Kramers-Kronigの分散式や各種の総和則,恒等式を,特定のモデルや近似によらない一般的な形で論ずることも可能になるのである.
熱平衡系の統計力学でも,自由エネルギーを系のハミルトニアンで表す公式があり,これにもとづいて熱力学の諸公式を再構築することができる.モデルや近似は,特定の系について比熱の温度変化,相転移等を論じたい場合に初めて導入される.線形応答理論でも事情は同様である.モデルや近似は,特定の系の電気抵抗やその温度変化等を知りたい場合に初めて導入される.
他方,非線形非平衡系の統計力学の対象には,強電場中の電気伝導のような通常の意味の非線形現象のみならず,粘性流体の乱流のように,マクロな微分法則に従いながら,非線形性のために偶然性を帯びる現象も含まれる.このように広範な対象を包括できる理論スキームは未だ確立されていないし,それが可能か否かさえ明らかではない.
さて,上述のような,明確な目的意識に裏打ちされた線形応答理論は,1950年代に我が国で確立された.関与したのは,大学院生を含む,当時の年齢で40歳以下の少壮研究者達であり,久保亮五はその中心的な存在であった.本稿の目的は,こうした線形応答理論成立前後の状況を,なるべく広範囲の会員諸氏に紹介し,その意義を評価して頂くことである.
当然のことながら,同様の目的の解説はすでにいくつか書かれている.ここでは,久保の協力者であったし,久保理論の熱心な解説者でもある橋爪夏樹の解説1)と,線形応答理論を推進した重要人物の一人,中野藤生の報告2)とを挙げておこう.いずれも,記述や主張に当事者ならではの迫力がある.一方筆者は,本稿の性格上,できるだけ“距離をおいた”記述を心掛けるつもりであるが,筆者も当時者の一人であった以上,おのずから限界がある.執筆に際して特に重要視したい点をあらかじめ列挙し,筆者自身の立場を明らかにしておきたい.
1) フォーマリズムよりも物理に重点をおく.実際,場の量子論やGreen関数法のコンセプトが普及した現時点で見れば,フォーマリズムとしての線形応答理論が明らかにしたことは,「摂動として加えた外場が,多体系の物理量の期待値に誘起する1次の変化は,系の遅延Green関数で表示できる」という,almost trivial な“数学的”結論に過ぎない.重要なのはその“物理的”意義の方である.電気伝導のような,Joule発熱をともなう“非可逆”過程が,Green関数のような“一見純粋に力学的”な表示によって記述できるという事実の発見,確認が重要なのである.力学法則の可逆性と熱現象の非可逆性を両立させるべく苦闘したBoltzmannから半世紀余を経て,非可逆過程の統計力学はようやくこの簡潔な表現に到達したといえよう.統計力学史上,画期的な成果である.
2) この成功にもかかわらず,線形応答理論の基礎づけには,実は一抹の不透明さが残っている.前項の明快な結論が得られたのは,熱平衡を破る摂動が外部電場のような“力学的攪乱”(mechanical disturbance) であって,摂動ハミルトニアンとして表示できる場合である.一方,金属,半導体の熱電現象から,温度勾配が電場と同様に電流を駆動することがわかっている.しかし,この“熱的攪乱”を表すような(温度勾配に比例する)摂動ハミルトニアンはもちろん存在しない.力学的攪乱の場合には“非可逆性”はマクロ系のGreen関数に集約されたのに対し,熱的攪乱の場合には発端の定式化の段階ですでに“一見純粋に純力学的”なアプローチが挫折するのである.
熱的攪乱を扱う方法はあとで詳しく論ずることにして,ここでは,線形応答理論の基礎づけについて,もっと一般的な立場から疑義を差しはさんだ高橋秀俊のコメントを引用しておきたい.高橋はわが国におけるこの分野の先駆者である.1952年,Gibbsの古典統計力学によって熱的揺らぎ (thermal fluctuation) の時間的相関を線形非可逆現象に結び付けている.3)密度行列を使う量子統計力学のフォーマリズムが,例えば伏見康治の論文4)からもうかがえるように,当時すでに我が国に定着していたにもかかわらず,高橋は敢て量子統計力学の導入を避けた.量子力学特有の,観測問題の困難が絡むからというのがその理由である.
実際,物理量の時間的相関を記述する量子力学的表式として,異なる時刻におけるHeisenberg演算子の(対称化された)積の期待値が一応考えられるが,観測による状態の不連続的な変化を本気で考えた場合,その物理的な解釈は簡単なものではなかろう.古典論との単純なアナロジーが成立するのは,おそらく熱力学や統計力学で“マクロ変数”と呼ばれている.特定のタイプの物理量に限られるとおもわれる.後年,こうした量子力学的観測をめぐる難問について,会誌のインタヴュアー小林謙二に「久保亮五さんなどは,そんなことはかまわずいろいろやってゆくから良いのではないか」と語り,5)高橋は後輩達のオプティミズムを容認した.
もうひとつ,Ohmの法則のようなマクロなレベルでの線形性,必ずしもミクロなレベルでの線形性(つまり外場による摂動ハミルトニアンを1次の摂動論で扱うことの妥当性)を保証するものではあるまい,という疑問を,1953年,東京・京都で開催された戦後初の理論物理学国際会議で高橋が提起し,6) Onsagerがコメントの形で回答している.実際上問題になるマクロな系のマクロな物理量については,マクロとミクロの線形性を等価と考えてよい,というのが回答の骨子である.同様の質問はその後も,例えば van Kampen により繰り返され,7)同様の回答が久保亮五・戸田盛和・橋爪夏樹の総合報告(1991年)にあたえられている.8)
筆者自身は,現状でこの種の抽象的な一般論を繰り返しても不毛だと思う.いま線形応答理論を支えているのは,数多くの具体的課題に対して収めた成果であり,発展の方向は非線形系まで視野にいれた熱的攪乱理論の建設であると考えている.
3) エピソードを多く取り込むほど本稿が読みやすくなることは確かだが,研究会等での伝聞や筆者自身の記憶は信頼度が低いのでなるべく避け,高橋秀俊のインタヴューのように,客観的な資料が残っていて,しかも一般の会員諸氏のアクセスが比較的容易なものを尊重することにしたい.本稿執筆にあたって特に重要視した資料は,雑誌『物性論研究』である.謄写版で発行部数も少なく,プライオリティーを主張する根拠にはならなかったが,戦後しばらくの間,研究者達の本音が聞ける情報交換の場として活用された.線形応答理論の研究結果も,本論文以前のラフなスタイルでこの雑誌に登場したことが多い.『物性論研究』は共同利用研究所である東京大学物性研究所の地下図書室に全巻所蔵されていて,部外研究者がアクセス可能な点も好都合である.
なお,同じく『物性論研究』に準拠しているものとして,一柳正和の総合報告を挙げておく必要がある.9) 1930年から30年間にわたる,わが国における非平衡統計力学研究の発展をレヴューした労作であり,本稿で触れることのできなかった多くの研究が紹介されている.
4) 以下,線形応答理論が形成されたプロセスを,「揺らぎと散逸」,「磁気共鳴」,「電気伝導」,「熱的攪乱」と,順次たどることにする.
2. 揺らぎと散逸
非平衡系統計力学の歴史には二つの潮流がある.Boltzmannの気体運動論に始まる流れと,EinsteinのBrown運動論に始まる流れである.線形応答理論は後者の発展した姿と見ることができる.
まず,系に力学的攪乱をひきおこす外力は,いつもパルスの重ねあわせとして表示できることに注意しよう.系の線形応答は,各パルスを単独に加えたときに系の示す応答の重ねあわせと見なせる.したがって,理論的には単独パルスに対する応答を知れば十分ということになる.これは,しかし,熱平衡系に“自発的に”発生する熱的揺らぎのダイナミックスを追及することと等価である.実際,単独パルスを加えた直後には,系の物理量は熱平衡期待値からの外れ,つまり揺らぎを示し,以後の揺らぎの運動は,外力0の,系固有のハミルトニアンによって支配される“自然運動”である.この点,熱平衡系に自発的に起こる揺らぎの運動となんら異なるところはない.
線形応答理論の物理的なエッセンスは以上の通りだが,これを数学的に表示するものとして,いわゆる揺動・散逸定理 (fluctuation-dissipation theorem) がある.その名の通り,外力下で起こるエネルギー散逸と熱平衡系で起こる揺らぎを結びつける定理である.1905年にEinstein10)の導いた“Einsteinの関係”は最も古くから知られた例であり,現在でもイオン伝導や半導体のpn接合の話に,モビリティーと拡散係数を結び付ける式として登場する.
粘性媒質中のBrown粒子のモビリティーをm(抵抗係数の逆数),拡散係数Dとすると,
![]()
第1式のkはBoltzmann定数,T は絶対温度であり,第2式のv (t)は時刻tにおける粒子速度,また以下カギ括弧は熱平衡期待値を意味する.つまり,熱平衡系における粒子速度の時間相関関数をFourier変換して速度の揺らぎスペクトルを求めれば,そのゼロ周波数成分が拡散係数をあたえるのである.なお,第1式は外場(例えば重力場)中で熱平衡にある粒子のBoltzman分布を,外場によるドリフトと濃度勾散による拡散のバランスの式に代入して得られる一般式である.他方,第2式は“白いノイズ”をもつLangevin方程式を解いて得られる.ただし,後述の久保公式との対応を見やすくするために速度で書いた.
このモデルは導体中の荷電粒子の熱運動にも適用できる.実際,熱雑音電流の時間相関関数のFourier変換をこのモデルで計算してみると,角周波数帯域Dw内に発生する熱雑音電圧の2乗平均は,回路の電気抵抗をR として,4kTRDwに等しいことがわかる.周知のNyquistの定理である.もっとも,Nyquist自身は1928年,熱力学第2法則のみを使うスマートな思考実験によってこの定理をみちびいている.11)なお,高周波数域または低温では,等分配則kTをPlanck分布則におきかえる.いずれにしても,通信技術の飛躍的な進歩に伴い,熱雑音が現実に問題となる一方で,逆にNyquistの定理の実験的検証も可能になった.
揺らぎと散逸に関して,もうひとつ欠かせない話題は,1931年にOnsagerが導いた相反定理である.12)古くから知られていた実例は熱電現象に関するThomsonの相反性だが,わかりやすい例は結晶の熱伝導である.結晶の熱伝導係数は一般に2階テンソルだが,対称性の低い結晶でも,すべて対称テンソルであることを実験が示している.この事実を結晶構造の幾何学的対称性から説明することは,もちろんできない.1931年にOnsagerが明らかにしたように,輸送係数の示すこの種の対称性は,輸送現象の担い手であるミクロな粒子の運動が,時間反転対称性をもつことに由来する.つまり,力学法則の可逆性が,非可逆過程を特徴づける輸送係数の対称性に反映しているのである.
この結論を導く際,熱平衡系に自発的に発生した揺らぎの運動は,平均において,外的攪乱に対し系が示す線形応答と同じマクロな輸送方程式に従うとOnsagerは考えた.いま一組の準マクロな力学変数 x 1, x 2,… を考え,すべて時間反転に対し不変としておこう.熱平衡系における揺らぎを記述する時間相関関数の運動は,系の寸法が大きい極限で,漸近的に次のように表すことができる(EinsteinのBrown運動モデルが最も簡単な例).
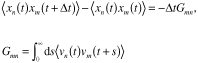
ただしvnはxnの時間微分である.その時間相関関数である第2式の被積分関数は有限な緩和時間tで減衰し,他方第1式左辺の時間相関関数の緩和時間はtよりはるかに長いとする.時間Dt は両者の中間に選んである(このような選択の可能なことが準マクロ変数の資格).
Onsagerは,上式のGmnをマクロな輸送係数と同一視することにより,力学法則の可逆性を利用して輸送係数の対称性Gmn=Gnmを結論したのである.なお,磁場中の荷電粒子の場合には,時間とともに磁場も反転したときに力学法則が不変になる.このため,磁場中の導体の電気伝導テンソルは,磁場0のときに0となるような反対称成分をもち,導体はHall効果を示すことになる.
熱平衡系におこる自発的な揺らぎが,マクロな輸送方程式(例えばエネルギーの揺らぎなら熱伝導方程式)にしたがって減衰するというOnsagerの仮定は,実質上,揺動・散逸定理を最初から前提とすることを意味する.後述するように,熱的攪乱まで含めて線形応答理論を展開しようとすれば,現在でもこのOnsagerの仮定が必要になる.線形応答理論によって揺動・散逸定理が一般的に証明されたと説く向きがあるが,間違いである.現状の線形応答理論は,揺動・散逸定理が成立するように構築されているのである.
3. 磁気共鳴の線形応答理論
我が国における線形応答理論の本格的な構築は,久保亮五・富田和久の磁気共鳴理論13)から始まった.1953年の理論物理学国際会議でその概要が紹介され,32ページにのぼる本論文は翌年の日本物理学会のジャーナル,11・12月合併号に掲載されている.本稿の執筆を担当したおかげで,久しぶりにこの迫力にみちた論文を読み返す機会にめぐまれ,上記国際会議組織委員でもあった久保,磁気共鳴分野の気鋭の理論家だった富田の若々しい面影を偲ぶことができた.
ところで,線形応答理論の構築が磁気共鳴から始まったのは偶然ではない.戦後急速に発展した NMR, ESR の実験は,静磁場におかれた凝縮系のスピン共鳴,特に共鳴吸収線の尖鋭化現象(narrowing)を新鮮な理論的課題として提供した.共鳴線の広がりは,スピン間の磁気的相互作用による周波数変調と見ることができる一方で,NMRの場合の核の熱運動やESRの場合の電子間交換相互作用は周波数変調を平滑化する高周波ランダム・ノイズとして働く.尖鋭化現象をこのようなランダム・プロセスとしてとらえたのは3人の実験家 Bloembergen, Purcell, Pound14) であり,量子力学的定式化と理論の定量化を進めたのは理論家のAndersonとWeiss15)であった.
“尖鋭化現象の物理”はこれで一応落着したのだが,統計力学の立場から見ると,それまで被平衡系を扱う標準的方法とされてきたBoltzmann以来の気体運動論や,これを凝縮系素励起へ拡張した輸送理論では処理できない,新しい課題が二つ提起されたのである.第1に,スピン共鳴の問題では,いうまでもなくスピン角運動量成分独特の交換関係が最初から基本的な役割を演ずる.しかし,量子力学的オブザーバブル一般の非可逆プロセスを扱う理論スキームは,当時まだ確立されていなかった.第2に,スピン角運動量に対するHeisenberg運動方程式から,GaussプロセスとかMarkoffプロセスとか,とにかくランダム・プロセスとして近似できるような非可逆的な運動が,如何にして導き出されるのか? Andersonは直観に訴えてランダム・プロセスを導入し,この数学的モデルとHeisenberg運動との関係には深入りしなかった.16)(当時Andersonは東京大学理学部久保研究室に滞在中だった).
久保・富田が以上の2点を明確に意識していたことは,論文の構成からも明らかである.Part A は上記第1の課題に対する回答であって,磁気分散・吸収の一般論ではあるが,実はスピン系を例にとって線形応答理論を展開したものと見ることができる.こうして,特定のモデルや近似に頼ることなく,スピン系の交流帯磁率がスピンの熱的ゆらぎを記述する時間相関関数,もっと正確にいえば,スピン系の2体Green相関のFourier変換で表される.
熱平衡にあったスピン系に,ある時刻t' を選んで弱いパルス磁場を加えたとする.時刻t '前の系を記述する密度行列はカノニカル分布であることがわかっているから,パルス磁場について1次の摂動論を適用して密度行列に対するNeumann方程式(Schrodinger方程式に等価)を解けば,時刻t>t 'における密度行列のカノニカル分布からのずれ,したがってまた,磁気モーメントの熱平衡期待値からの揺らぎを表す式が得られる.これとパルス磁場との比(2階テンソル)をGmn(t−t ')と書こう.久保・富田が応答関数と呼び,場の量子論では遅延Green関数と呼ばれる量である.角周波数wの交流磁場もパルス磁場の重ね合わせとして表示できることに注意すれば,複素交流帯磁率はGreen関数のFourier変換であたえられることがわかる.
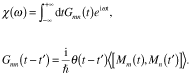
q(t )はt が正のとき1,負のとき0に等しい階段関数であり,Mm(t )は(パルス磁場が0のときの)磁気モーメントの“自然運動”を表すHeisenberg演算子である.
前節の古典論的表式との対応を見るには,時間について部分積分して次のように書いた方がよい.
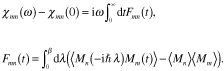
bkT=1である.Fmn(t
)は,時刻t=0に静磁場をわずかだけ不連続的に変えたとき,磁気モーメントに対するその影響が時間の経過とともに減衰する様子を記述する量であって,緩和関数と呼ばれる.b![]() →0の極限で古典的な相関関数のb倍に帰着し,(磁性体の場合の)高橋秀俊3)の古典論が再現される.
→0の極限で古典的な相関関数のb倍に帰着し,(磁性体の場合の)高橋秀俊3)の古典論が再現される.
ここで得た“一見純粋に力学的な”表式の何処に“非可逆性”が潜んでいるか? 物理的には揺らぎが速やかに減衰すること,数学的には(粒子密度を一定に保って系の体積を無限大にしたあとで)t →+∞の極限で緩和関数が0に収束することが非可逆性の表現である.Khinchinによれば,この条件は,いま問題にしている物理量についてエルゴード定理が成立することと等価である.17)
Part A は密度行列の運動方程式を,カノニカル分布を初期条件とし,力学的攪乱について1次の摂動論で解いたものであり,非可逆過程論にありがちな曖味さは全くない.Part B は,上述のGreen関数に現れるHeisenberg運動から,ランダム・プロセスとして近似できるような様相を如何に導き出すか,いわば非可逆過程の核心に触れる部分であるが,ここでも論理は明晰である.
静磁場によるスピン・Zeemanエネルギーを無摂動ハミルトニアン,スピン間相互作用を摂動と見なし,Heisenberg演算子を摂動展開する(量子電気力学で開発されたこの種の技術は,当時すでに物性理論にも輸入されはじめていた).しかし熱的揺らぎの減衰を支配する長時間のふるまいを知るためには,摂動展開のままでは役に立たない.展開の諸項を適当にまとめ,“もう一度指数関数の肩に乗せる”必要がある.正確にいうと,緩和関数の対数を無次元結合定数のベキに展開(キュムラント展開)したと考え,展開係数を摂動展開と比較して求めるのである.この方法により,半ば物理的直観によって導入されたランダム・プロセス・モデルが基礎づけられたばかりでなく,さらに精密化されたのだが,詳細 (Part C) は割愛する.
4. 電気伝導の線形応答理論
磁性体のスピン・ダイナミックスと違って,金属電子系の電気伝導は,Boltzmann方程式による伝統的なアプローチがFermi流体で成功を収めた模範例である.この問題に線形応答理論を適用すれば,最も単純な近似の段階ですでに伝統的な方法と同じ結果が得られることを,中野藤生が1955年に実証した.18)
熱平衡にあった導体に,時刻t =0に(単位の強さの)パルス電場を加えたとする.以後の時刻における電流のHeisenberg演算子Jm(t )の期待値が緩和関数,そのFourier-Laplace変換が交流電気伝導度テンソルである.

中野によって最初に導かれたこの表式は,明らかに§2で述べたEinsteinの関係の量子論版である.現在では電気伝導度に対する“久保公式”と呼ばれることが多い.
中野はこの表式に電子・フォノン系のハミルトニアンを代入し,電子・フォノン相互作用について2次までキュムラント展開することによって,固体物理のテキストに載っている高温電気抵抗の表式を導いた.当時英国滞在中だった筆者は,送られてきた雑誌『物性論研究』の中野の論文にショックを受け,早速この方法が低温までうまく機能することを確かめた.19)周囲の人々にもこのニュースを伝えたが,反応はさまざまで,FrohlichやSchafrothは積極的に評価,Peierlsは消極的だった.20)同じ頃,直接に中野から話を聴いたFeynmanは,来日の機上で自ら導いた結果ということで,エネルギー表示snn(0)の一般式を,自筆メモの形で中野に遺している.2)
その後の国内の研究の展開にとって,中野の発見は“コロンブスの卵”であった.まず,雑誌『物性論研究』に載った久保のコメントによれば,中嶋の電気抵抗計算は電子・フォノン系におけるHeisenberg運動のランダム化を最低近似で示したものであり,実はBoltzman方程式も同じレベルのランダム化を別の形で表現しているに過ぎないから,両者が同一の電気抵抗をあたえるのは当然である.21)ここでは久保・富田の Part A のスキームが電気伝導に転用できることは,もはや自明の理とされているのである.
実際,『物性論研究』の同じ号に載った「非平衡系の量子統計力学 I--Fluctuation-Dissipation Theorem と Correlation Function の方法」と題する論文で,久保は線形応答理論のスキームを磁場や電場以外の力学的攪乱も含む一般的な形に定式化し,緩和関数,相関関数あるいはそれらのFourier変換について,恒等式,総和則,分散式,相反定理等を特定のモデルや近似に依存しない形で導いている.22)“久保理論”の名に最もふさわしい内容である.その前後,久保はこうした一般論と,定式化そのものやHeisenberg運動のランダム・プロセス化に近似を含む“近似論”との区別を強調し,筆者もこれに同調した時期があった.
例えば,当時,森 肇がユニークな非可逆過程の量子統計力学を展開しつつあった.23)局所平衡を表す密度行列を初期条件として,ミクロには長く,マクロには短い時間Heisenberg運動を追跡する.Onsager理論同様に力学的攪乱も熱的攪乱も同等に扱い得るよう定式化されているが,力学的攪乱に話を限れば,定式化は近似論ということになろう.この問題には次節でもう一度立ち返る.
誤解がないように付言するが,久保は近似論を低く見たわけではない.同時期に強磁場におかれた電子軽の磁気抵抗,Hall効果の問題をみずからアタックし,また門下の俊秀を動員している.彼らの健闘ぶりは,橋爪の解説1)および本誌久保博士追悼号の三宅哲の項24)に紹介されているので,ここでは立ち入らない.磁場には垂直な面内の電子運動が量子化されていて,この問題は伝統的な処方箋で扱いにくい難問である一方,(ずっと後になってわかることだが)2次元系なら量子Hall効果や分数量子統計につながる魅力的な課題でもある.しかし,当時は近似方法も物理的コンセプトも十分には熟成していなかった.
これと関連して筆者がいまも残念に思うのは,ちょうど同時期に提案された松原武生の温度Green関数25)(虚数時間軸上で定義されたGreen関数)を線形応答理論に活かす努力が,あまり発展しなかったことである.松原の動機が,場の量子論の摂動展開(Feynmanグラフ)を有限温度系に拡張するという“近似法”の開発にあったためかもしれない.Fermi粒子あるいはBose粒子の1体温度Green関数の周期性(したがってFourier級数展開の可能性)を江沢洋・友沢幸男・梅沢博臣26)が指摘し,Bloch de Dominicis27) およびAbrikosov・Gro'kov・Dzyaloshinskii28)によって温度Green関数法は一挙に実用化された.当時,磁気抵抗の赤外発散に悩まされていた久保研究室から橋爪が梅沢を訪ねた由であるが,残念ながら固体物理・場の量子論協力の機は熟していなかったようである.
例えば,先に述べた電気伝導度テンソルの一般式は,実時間の2体Green関数を使って次のように書ける.
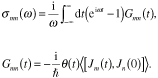
Abrikosovらによれば,第1式のG のFourier変換は,対応する温度Green関数のFourier変換を複素周波数面上で解析接続することによって得られる.温度Green関数についてFeynmanグラフによる摂動展開の分析が可能であり,Heisenberg運動のランダム・プロセス化を“視覚的に”処理することができる.詳しくは,本誌“50年をかえりみる”シリーズの阿部龍蔵「統計力学におけるGreen関数」の明晰な記述を参照して頂きたい.29)
このように実用化された温度Green関数法は,Anderson局在のような,明らかにBoltzmann方程式の枠を超えた問題にまで威力を発揮することになった.30)一般論,近似法,物理的コンセプトが相互に絡み合って進歩するところに,物性理論の特質を見ることができよう.
5. 熱的攪乱の問題
現実の金属,半導体では電場が熱流を駆動し,温度勾配が電流を駆動するだけでなく,これらの交差現象の輸送係数の間にOnsagerの相反定理が成立している.力学的攪乱をめぐる一般論の美学に酔って熱的攪乱の問題を放置しておくことはできない.実際,論文Iに引き続き,久保は横田万里夫との共著「非平衡系の量子統計力学II―熱的なdisturbanceに対するresponse」を雑誌『物性論研究』に載せた.31)熱的攪乱を表す摂動ハミルトニアンが存在しないために,論文Iの演繹的な理論の展開が論文IIでは帰納的な模索に替わる.簡単な自由電子モデルについて論じているが,以下の論議はモデルにはよらない.
熱的攪乱を含む線形応答理論の定式化として,二つの可能性を検討する.第1は,§2で述べたOnsager理論を量子論の言葉に読み替えることである.久保・横田は,揺らぎを記述する相関関数に含まれる2個の物理量は量子力学的演算子とみなし,両者の積を対称化すればよいと考えた.しかし,その結果得られる電気伝導度テンソルは,§4に示した一般式と対称部分は一致するが,反対称部分(Hall効果)が食い違う.§4で示した電流緩和関数F の表式で,lに関する積分が単なる因子bと演算子の積の対称化操作に置き替わってしまうからである.つまり,高温または古典極限でのみ正しい結果ということになる.
そこで第2の可能性を検討するわけだが,温度勾配や電子密度勾配の存在する場合のBoltzmann方程式の解法を真似るのである.密度行列を温度勾配や電子密度勾配をもつ局所平衡の状態を表す項と,それからのずれを表す項の和の形に仮定し,Neumann方程式の定常解を求める.その際,一部で電子・フォノン相互作用を無視するなど,定式化の段階ですでに“近似論”である.結果として得られる電気伝導度テンソルは本稿§4の表式と形式上一致するが,後者のような一般性を主張することは到底不可能である.
ところで,第1案の挫折について,“議論にはどこか欠陥があると思われる”と久保・横田が『物性論研究』に書いているのを読み,筆者は改めてOnsagerの論文に立ち戻ってみた.Onsagerの相関関数は(演算子の対称積に読み替えても)量子論では物理的にあまり意味がなく,これを直輸入したことが久保・横田理論の欠陥だと気づいた.前論文Iの副題からも窺われるように,確率過程論に通暁していた久保には,相関関数が基本的な量という直観があったのかもしれない.
熱平衡系で,例えば時刻t =0に,準マクロ力学変数xが熱平衡値0からの揺らぎx 'を示したとする.それ以後の揺らぎの運動は“平均において”マクロな輸送方程式に従う,というのがOnsagerの仮定である.xの揺らぎがx 'という条件を満たすミクロな状態はむろん無数にあり,これについて平均をとるのである.Onsagerはミクロ・カノニカル分布について平均したが,ここでは物理的にそれと等価で,しかも量子論での扱いが容易なカノニカル分布を採用する.
xおよびハミルトニアンH の期待値をそれぞれ一定にしてエントロピーS を最大にする密度行列は,
![]()
定数 a, b, W は上記の期待値と密度行列の規格化条件できまる.bが温度の逆数であることはいうまでもない.aはエントロピーを揺らぎx 'で微分したもので,非可逆過程の熱力学でx 'に共役な駆動力とよばれている量である.
揺らぎx 'は小さいとし,aについて展開して1次の項だけ残せば,時刻Dtにおける揺らぎは次のようになる.
![]()
右辺の“ラムダ積分”は非可換演算子の指数関数の展開に付き物であって,古典的極限でのみ相関関数をあたえる.こうして久保・横田理論の欠陥が除去されるのである.
以上述べた筆者の理論は『物性論研究』に載せたが,32)久保の要請により,久保,横田,中嶋のジョイント・ペーパーとして公表されている.33)これは余談になるが,その後,Enrico Fermi 夏の学校で非可逆過程論がとりあげられた.筆者も久保の推薦で参加の機会を得,Onsager, Kirkwood, de Groot その他,当時の大家の講義の間にはさまって,上記の研究を報告した.1週間の滞在中,晩餐はいつもOnsagerが筆者に差し向かいに座るよう命じ,"kill the bottle'' と2人でワインを1本空けることになっていた.もっぱら彼のワイン談義を聴かされ,あまり物理の話をした記憶がない.ただし,熱的攪乱についてはまだ問題が残っていると思うがと尋ねたところ,"No. You and Kubo have cleared it" と答えたのは覚えている.
それにもかかわらず,実用上はともかく,線形応答理論の基礎づけが不十分だという筆者の印章はいまも変わっていない.これまで述べたことを要約すれば,次の通りである.力学的攪乱については,久保の一般論はもちろんのこと,磁気共鳴吸収,電気伝導からAnderson局在まで,理論の構造はcrystal clearであり,“力学的”である.“統計”が参入する場合でも,その場所と理由は明らかに特定できる.ところが,熱的攪乱の場合には,これを摂動ハミルトニアンとして表示できないために,理論は定式化の段階からすでに不透明になってしまう.
ところが,困ったことに,自然は意地悪くも導体の電気伝導と熱伝導を連立させ,両者を相反定理で結びつけている.理論も両者を対等に扱いたいわけである.この要求を現状で満足させようとすれば,Onsagerの仮説を認めて力学的攪乱も熱的攪乱も差別なく扱うしかない.あるいは§4でのべた森理論を採用しても実質は同じことである.いずれにしても,力学的攪乱については久保の一般論と矛盾しては困るわけで,その意味で後者はチェックの役を務めることになる.
もうひとつの可能性として,熱的攪乱に対する応答理論を現状よりもっと“力学的”にする方向が考えられる.力学的攪乱の場合,温度Green関数法によって場の量子論を多体問題攻略の有力な武器とすることができたわけだが,高橋康・梅沢博臣の Thermo Field Dynamics は統計力学のフォーマリズムそのものを場の量子論の形に定式化するユニークなアプローチであり,34)熱伝導や拡散への応用が江沢洋らによって試みられている.35)
一方,古典力学の範囲内ではあるが,マクロな力学系の示す偶然性の起源を力学系に内在する不安定性,カオスに求める研究が発展している.熱平衡系統計力学を基礎づけるエルゴード定理から始まって,最近ではHamilton力学系の拡散係数その他の輸送係数をカオスの特性指数で表示するところまで進んできた.解かりやすくいえば,§2のBrown運動論ではBrown粒子に働くランダムな力を現象論的に導入するのだが,その正体は実はカオス的な散乱だというのである.もしそうなら,熱的攪乱に対するOnsagerの仮定は不要になるものと思われる.もっとも,量子論との折り合いをどうつけるかという問題は残るが.
しかし,統計力学の現状や近未来を語ることは本稿の役割ではないし,筆者の能力を超えた課題でもある.会誌久保博士追悼号に寄せられた北原和夫のシャープな解説を参照していただききたい.36)北原も指摘しているように,非平衡系統計力学はいま新たな発展期を迎えており,わが国からの創造的な寄与を大いに期待したいところである.
6. おわりに
当初構想を建てた段階では,もう少し展望の広いレヴューを書くつもりであったが,結局,1950年代中期の,しかも筆者の身近で起こった研究の発展のみ詳しく紹介する結果となった.“50年をかえりみる”という標題には背いたかもしれない.冒頭に,なるべく距離を保つよう努力すると書いたが,これもあまり確かではない.
しかし,一方からいえば,戦後10年という時期に,久保亮五を中心とする若手研究者の小グループが展開したきわめてユニークな理論研究である.e-mailも Phys. Rev. Lett. も気にせずに,グループ内の情報交換でおよその用が足りた,現在では想像もできないような時代であり,研究であった.これを紹介するためには,本稿のスタイルもあながち見当はずれでないかも,と思いなおしている.もっと長期にわたるグローバルな研究の発展については,適切な著者の精密な報告を期待したい.§6で述べた熱的攪乱をめぐる新しい研究動向も,そうしたフレシュな報告を必要とするテーマの一例である.これについては,統計力学分野担当の北原和夫前会誌編集委員から教示を受け,できれば共著をお願いしたいと考えていたが,筆者の怠慢で不可能に終わった.
かえりみると,本稿の執筆依頼を受けたのは江沢洋先生が会誌編集委員長をしておられた頃である.このテーマの執筆者として久保亮五先生が最適であることはいうまでもないが,当時すでに先生は重篤の病床にあり,本稿の構想について先生の批判を仰ぐこともできないまま逝去された.会誌が先生の追悼号を計画中に聞いてしばらくの間待機し,門下生の皆さんの追悼文を拝見した上で執筆にとりかかった次第である.
筆者の身勝手のために,湯川哲之委員長はじめ会誌編集委員会の諸先生方にはご心配をかけてしまった.北原前委員のご協力とあわせて,感謝とお詫びを申し上げたい.また,適切なコメントを沢山頂いた江沢先生に厚くお礼申し上げる.
最後に,"Kubo is a great physicist" という.30年以上も前にKadanoffから聞いた言葉を添えて,先生のご冥福を祈りたい.
参考文献
- 橋爪夏樹:『統計力学の進歩』久保教授還暦記念事業委員会編(裳華房,1981)
- H. Nakano: Int. J. Mod. Phys. B 7 (1993) 2397.
- H. Takahashi: J. Phys. Soc. Jpn 7 (1952) 439.
- K. Husimi: Proc. Phys.-Math. Soc. Jpn. 22 (1940) 264. 揺動・散逸定理の量子論版としてよく引用されるのは,H. B. Callen and T. A. Welton: Phys. Rev. 83 (1951) 84.
- 高橋秀俊:日本物理学会誌 40 (1985) 179.
- H. Takahasi: Proc. Int. Conf. Theor. Phys., Kyoto (1953) p. 488.
- N. G. van Kampen: Phys. Norv. 5 (1971) 279.
- R. Kubo, M. Toda and N. Hashitume: Statistical Physics II (Springer, 1991) Chap. 4.
- M. Ichiyanagi: Phys. Rep. 262 (1995) 227.
- A. Einstein: Ann. Phys. [4] 17 (1905) 549.
- H. Nyquist: Phys. Rev. [2] 32 (1928) 110.
- L. Onsager: Phys. Rev. 37 (1931) 405, 38 (1931) 2265.
- R. Kubo and K. Tomita: J. Phys. Soc. Jpn. 9 (1954) 888.
- N. Bloembergen, E. M. Purcell and R. V. Pound: Phys. Rev. 73 (1948) 37.
- P. W. Anderson and P. R. Weiss: Rev. Mod. Phys. 25 (1953) 269.
- P. W. Anderson: J. Phys. Soc. Jpn. 9 (1954) 316.
- A. I. Khinchin: Mathematical Foundation of Statistical Mechanics (Dover, 1949).
- 中野藤生:物性論研究 88 (1955) 25. H. Nakano: Prog. Theor. Phys. 15 (1956) 77.
- 中嶋貞雄:物性論研究 88 (1955) 45.
- 中嶋貞雄:固体物理 20 (1985) 489.
- 久保亮五:物性論研究 89 (1955) 72.
- 久保亮五:物性論研究 89 (1955) 79. R. Kubo: J. Phys. Soc. Jpn. 12 (1957) 570. なお久保理論をGreen-Kuboとして引用することがしばしばあるが,久保の分類でいえば,Green理論は“近似論”である.M. S. Green: J. Chem. Phys. 20 (1952) 1281, 22 (1954) 398.
- 森 肇:物性論研究 90 (1955) 25, 193, 92 (1956) 32.
- 三宅 哲:日本物理学会誌 50 (1995) 873.
- T. Matubara: Prog. Theor. Phys. 14 (1955) 351.
- H. Ezawa, Y. Tomozawa and H. Umezawa: Nuovo Cim. 5 (1957) 810.
- C. Bloch and C. de Dominicis: Nucl. Phys. 7 (1958) 636.
- A. A. Abrikosov, L. P. Gor'kov and I. E. Dzyaloshinskii: Sov. Phys.-JETP 9 (1959) 636.
- 阿部龍蔵:日本物理学会誌 50 (1995) 252.
- H. Fukuyama: Electron-Electron Interactions in Disordered Systems (North-Holland, 1985) p. 155.
- 久保亮五,横田万里夫:物性論研究 89 (1955) 99.
- 中嶋貞雄:物性論研究 102 (1956) 24, 104 (1957) 6.
- R. Kubo, M. Yokota and S. Nakajima: J. Phys. Soc. Jpn. 12 (1957) 1203.
- Y. Takahashi and H. Umezawa: Collective Phenomena 2 (1975) 55.
- H. Ezawa: Progress in Quantum Field Theory, ed. H. Ezawa and S. Kamefuchi (Elsevier, 1986) p. 305. K. Watanabe, K. Nakamura and H. Ezawa: Thermal Field Theories, ed. H. Ezawa, T. Arimitsu and Y. Hashimoto (Elsevier, 1991) p. 79.
- 北原和夫:日本物理学会誌 50 (1995) 891.