|
|
| 50年をかえりみる |
原子核構造理論の発展と現在--殻模型を中心として--
有馬朗人
〈理化学研究所 351-01埼玉県和光市広沢2-1〉
戦後より現在まで50年間の原子核構造理論の発展における日本の寄与について述べる.その際殻模型を用いた研究に主な焦点を当てて議論を進めていく.
1. 黎明期
原子核の基本的性質
原子核の基本的構成粒子は陽子と中性子である.今日では核子(陽子及び中性子)は更にクォークから成立していることが明らかになってきた.現在の最前線の問題の一つは,クォークから原子核がどのように形成されるかであるが,まだその途は遠い.この小論では従って陽子と中性子から原子核が作られているという,古典的描像を中心に話を進める.一つの原子核で陽子の数をZ,中性子の数をN,和を質量数と呼び,通常それをAと書く.A=Z+Nである.
原子核の半径は
![]()
従って体積VはAに比例している.このr0は初期にはa粒子の散乱断面積の分析などから1.4×10-13 cmと思われていたが,1953年Rainwaterたちのm原子のエネルギーの測定や電子散乱の断面積の測定によって現在の値に定着したのである.また結合エネルギーは
![]()
である.この二つの性質は原子核の飽和性と呼ばれる.
飽和性を示す巨視的物体は水滴である.そこで原子核の液滴模型が N. Bohr たちによって提案され,それを用いたWeizsacker-Betheの質量公式1)
.gif)
は現在でも第一次近似としてよく用いられている.原子核の分裂はHahnらによって発見されたが,2) BohrとWheeler3)は液滴模型に基づいて,この現象を理論的に解明したのである.
原子核の魔法数の発見
液滴模型によれば原子核の性質は,ZやNになだらかに依存するだけである.ところがさまざまな原子核の存在量や,核反応の断面積はZやNにかなり鋭敏に左右される場合があることが判ってきた.特に特定の数のとき原子核の安定性が大きくなる.その数を原子核の魔法数と呼んでいる.それは
![]()
である.ただしZ=126はまだ作られていない.N=126を越えた所にも魔法数があるかも知れない.そういう超重元素を探ることは最先端の問題である.
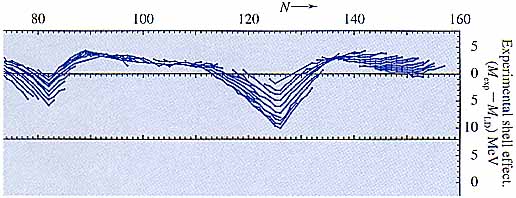
魔法数の存在を一番はっきり示すには,質量の実験値から先程の質量公式による理論値を引いてみるのが良い.図1はその結果である.この差はせいぜい10 MeVで,1,000MeV前後の大きな結合エネルギーに比べて,小さな量であるが,魔法数のところで結合エネルギーが大きくなることが明瞭に判るであろう.
天然にはZ=92のウラニュームまでであるが,現在はZ=110まで存在することが確かめられている.陽子や中性子を放出する原子核を人工的に作る努力が現在盛んに行われているが,核子の放出に対して安定な原子核は,ほぼ3,000種あると考えられている.
j-j結合殻模型
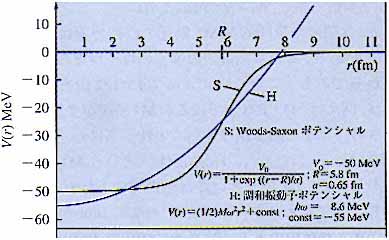
原子核の魔法数の存在は,原子と同じように原子核も殻構造を持っていることを示している.核内の核物質の密度はほぼ一定であるから,核内核子が作る平均場は図2のような滑らかなものである.Wignerはこのような模型で 2, 8, 20 の魔法数を説明した.4)ところがそれ以上の魔法数は説明できなかった.そこでMayerとJensenは独立に,平均場に強いスピン軌道力
![]()
を加えることによって,28以上の魔法数を見事に説明したのである.5)球形な平均場内の核子はその軌道角運動量lを量子数として持つ.その平均場に強いスピン-軌道力が加わると,軌道とスピンが結合してj (j=l+s)が良い量子数になる.そこでMayerとJensenの殻模型をj-j結合殻模型と呼ぶ.一方,WignerのものをLS-結合殻模型と呼んで区別している.16Oより軽い核ではLSの方が第一近似として優れている.j-j結合殻模型は,中重核や重い核のスピンや磁気双極子能率を見事に予言した.
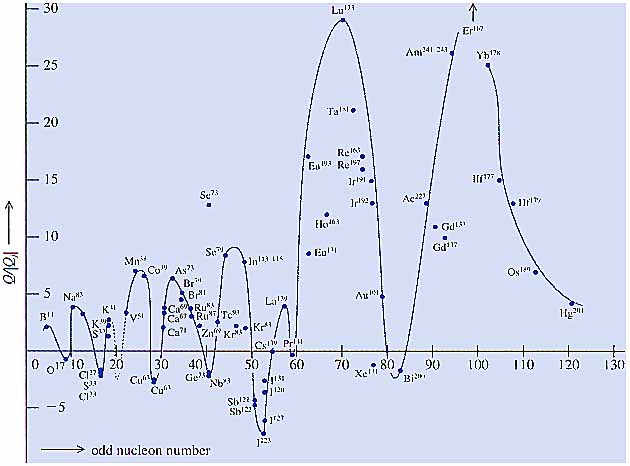
質量公式の第2項は表面張力項であった.この力により原子核は球形になろうとする.特に魔法数を持つ原子核−それを閉殻核と呼ぶが−は球形になる.そこで電気四重極能率は,閉殻外の陽子の分布が持つ球形からのずれに比例していると考えられていた.実はここに二つの問題が含まれていたのである.閉殻外の核子が球対称の平均場を廻転していて全体にほぼ球形に分布する.そして最後の1核子だけが電気四重極能率を持つという.単一粒子近似では到底説明できない程大きな値を持つ核が発見されたのである.その典型は175Luであった.これが第一の問題であった.もう一つの問題は17Oのように閉殻外に1個電荷のない中性子を持つ核が,かなり大きな電気四重極能率を持つことであった.即ち一方でj-j結合殻模型は,原子核のさまざまな性質を見事に説明しつつあった時に,早くもこのようなほころびを見せていたのである.
変形核と回転運動の発見
巨大な電気四重極能率の問題はRainwaterによって解決された.6)その考えによれば,ある種の原子核は楕円体にゆがんで,単一の陽子だけでなく多くの陽子が四重極能率に寄与するというのであった.ちなみにRainwaterは物理学者としてごく数の少ないアメリカ・インディアンである.この考えを発展したのが A. Bohr とその協力者の B. Mottelson であった.核は変形すれば回転運動がある筈であるとBohrは予言し,それは見事に実証された(図4).巨大な四重極能率の存在と,回転レベルの存在は,楕円変形した原子核を明瞭に証明したのである.7)
Rainwater-Bohr-Mottelson模型のはなばなしい成功は,球対称の平均場の代りに四重極変形した場―通常異方性のある調和振動子場で近似する―での単一粒子レベルに示された.これはNilssonによって計算された.8)このNilsson模型の予言は,重い変形核のスピンの実験値と実に良く一致し,変形核の概念を確立したのである.
|
| 図1 原子核の質量の実験値(Mexp)と液滴模型質量公式による予言値(MLD)との差を中性子数(N)の関数として図示した.(W. D. Myers and W. J. Swiatecki: Annu. Rev. Nucl. Part. Sci. 32 (1982) 309 による.) |
|
|
図2 核子に対する一体ポテンシャルの例. |
|
|
図3 電気4重極モーメントの観測値(Q)と Qj= 2j−1 2j+2 3 5 r20A2/3 との比.r0=1.2×10 −13 cm としてある. |
 |
|
図4 回転核の例.( )内の数字はE=aI(I+1)を仮定し,2+のエネルギーでaをきめたときの予言値. |
2. 殻模型の精密化
磁気双極能率と有効電荷
j-j結合殻模型の成功点の一つは核のスピンと磁気双極能率を良く説明できることであった.単一粒子模型によれば,軌道角運動量lでスピンjの核子の磁気双極能率は
![]()
で与えられる.これをSchmidt値と呼んでいる.きわめて多くの奇A核の磁気能率は奇陽子核,奇中性子核それぞれ2本のSchmidt線に挟まれた領域に分布する.その外へ出るのはごく軽い 3H, 3He, 15N 等ごく少数の核に過ぎない(図5参照).
ところでもしこの模型が完全に正しければ,実験値は2本の線のどちらかに乗る筈である.しかし現実にはかなりそれからずれている.この問題に世界的に最も早く挑戦したのは宮沢弘成であった.9)宮沢は核子間にPauli禁止則が働くため,パイオンの寄与が核内で変わることを指摘したのである.これはパイオン交換流についての先駆的な仕事であった.宮沢はgsが大きく変化することを予言したが,これはやや大きく評価し過ぎであった.しかしglが10%程度陽子で大きくなり,一方中性子では−0.1ぐらいになるという予言は,15年程後になって山崎敏光たちの実験によって確認されたのである.10)
一方,堀江久と有馬は1953年当時,きわめて安定と考えられていたj-j閉殻に核子をつけ加えることによって,いわばスピンの潮汐運動が起る可能性に気がついた.その結果,殻模型の波動関数f(jm)は,
![]()
という風に配位の混合が起ると考えたのである.ここでj−11は閉殻にあるj1なる軌道に孔があいたこと,j2はそれが閉殻外のj2軌道に励起したこと,lはこの1孔-1粒子状態が持つ角運動量である.aは混合振幅で小さいとする.j1=l1+1/2, j2=l1−1/2 でl=1であると,aが小さいにもかかわらずこの混合は大きくmを変化させる.その理由はmsをSchmidt値として
![]()
でdmは閉殻の集団的なM1励起の行列要素に比例するからである.すなわち閉殻内の多くの粒子がそろって貢献するからである.このことによってl±1/2両方が閉殻である核,例えば 17O, 17F などではこのM1励起がないのでdmが小さい.しかし陽子側はh11/2,中性子側はi13/2まで閉殻の209Biでは h−111/2 h9/2(1+), i−113/2i11/2(1+) というM1励起が可能であるから,dmが大きいことを説明できたのであった.11)同じような考えは少々早いくらいに R. Blin-Stoyle によって提案されたのである.12)当時はプレプリントがまだ流行せず,雑誌も船便で来た.我々にとって幸いなことであった.
209Biのdmが大きいという謎はこうして解けたかに見えたが,上述の1次効果―有馬・堀江効果―のみでは足りないこと,17Oや41CaなどLS閉殻±1核子核といえどもdmが0でないことが明らかになり,高次の補正と交換流の重要性が議論に登場したのは1970年前後のことである.Chemtob13)による宮沢効果の再発見(dg1=±0.1),交換流について日向裕幸たち14)やTownerとKhanna15)の精細な計算が一方にあり,一方清水清孝,市村宗武と有馬の2次の摂動効果の重要性の指摘があった.16)この2次の効果で重要な働きをするのはテンソル力であるので,テンソル相関と呼ばれることがある.この効果は許容型b崩壊―例えば 17F→17O, 41Sc→41Ca―で重要な役割をすることが判った.これは後にGamow-Teller転移に関して大論争の要因となった.
glの変化dglと電気双極巨大共鳴の和則への交換流の寄与(k)という一見全く繋がらない二つの量の間に,比例関係があることを故藤田純一と平田道紘が発見した.17)これを藤田・平田の関係式と呼ぶ.
![]()
kは古典的和則からのずれである.ところが和則の実験値からはk=0.1の程度,従ってdglは0.2程度になる.しかし実験によるとdgl=0.1である.そこで有馬は G. E. Brown, 日向裕幸,市村宗武と協力して藤田-平田の関係式を補正したのである.18)
話が再び1954年頃に戻るが,(1)式の配位混合で閉殻内陽子j1が,閉殻外のj2に励起し,lp=2+(pはパリティ)という1孔-1粒子状態を作ると,閉殻外の核子が中性子でも有限の電気四重極能率(Q)を持つことになる.この計算は1955年に堀江久と著者で行われた.19)この時17OのQは−0.04×10−24cm2と予言したが,当時の実験値は−0.004×10−24cm2と遙かに小さかった.しかし後にTownesが実験しなおして−0.027×10−24cm2と我々の予言に近い値を得たのであった.20)こうして中性子が有効電荷deN〜0.5e,陽子がe+dePでdeP〜(0.3〜0.5)eを持つことが理論的に導かれたのである.似た考えはAmadoが出している.21)
この配位混合の考え方は,lp+の状態としてスピンlの巨大共鳴をとることによって,もっと概念を一般化することができる.そこでこのような効果は芯偏極効果と呼ばれるようになった.この一般化においてはBohrとMottelsonの寄与が大きい.22)事実磁気能率に対する有馬-堀江効果を最初に認めてくれたのは,この二人とイスラエルの de Shalit とTalmiであった.
この芯偏極効果は佐野光男たちによってl-禁止M1転移や,23)堀江-有馬によってl-禁止b崩壊,24)そして浜本育子によって許容型b崩壊に応用された.25).
多粒子殻模型
4Heから16Oまでは0p-軌道が占拠されるので,p-殻核と呼ばれる.初期の段階でInglisやKurathは,0p-軌道にいる核子間に2体の相互作用を導入し,更に1体のスピン-軌道力を加えたハミルトニアンを対角化する計算を行った.LSとj-jの中間にあるので,中間結合殻模型と呼ばれたものである.26)しかし本格的な配位混合による多粒子殻模型の計算はElliottとFlowersによるものであった.27) 16Oを閉殻として,それに2核子付加した 18O, 18F, 3 核子付加した 19O, 19F のエネルギーの計算であった.これらの核子は0d軌道と1s軌道に入っている.有効相互作用としての現象論的な2体力とスピン-軌道力の強さをパラメタにして,低いエネルギー準位の実験値を再現することに成功した.
この結果に励まされて日本でも有馬は井上健男,瀬部孝,萩原仁の諸氏と協力して,0d-1s軌道に4個核子が入る核,20O, 20F, 20Ne の構造を計算した.28)世界で初めて20Neのレヴェル構造の計算に成功し,実験値に良く一致する結果が得られたことは嬉しかった.日本の大学にはまだ2K語のパラメトロン型の計算機しかなく,それを用いて50次元ほどの対角化を行ったのであった.このとき我々は2陽子-2中性子系が核内できわめて安定であること,20Neは16Oの周りにa粒子が廻転しているというクラスター描像と,殻模型の描像がよく似ていることを認識したのである.この事実は後述するaクラスター・グループの活躍と殻模型グループが協力する一つの起因であった.
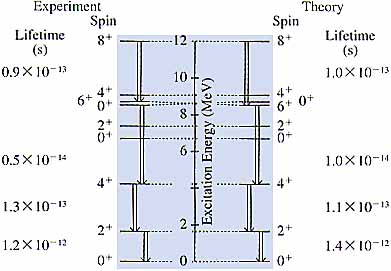
ところでElliottとFlowersそして井上-瀬部-萩原-有馬と共通に成功したと思われていた18F(=16O+p+n)の構造で不思議なことがあった.それはどんなに2体力のパラメタを変化かさせても,1.7MeVにあるスピンが1でパリティ+の準位を説明できなかったのである.勿論基底に近い低い準位には問題なかった.しかし殻模型によれば1.7MeVあたりには準位がなく,それ以外の準位はそれよりずっと高い所にしか予言できなかった.
その前後アメリカのArgonne研究所の Cohen, Lawson, MacFarlane と曽我は,当時最高の計算機を駆使し,また,1粒子エネルギーや2体の核力の行列要素パラメタとし,それをχ2法で実験に合わせる方法をとって,N=50で38≦Z<50の原子核の構造を説明することに成功した.29)大規模殻模型計算の走りであった.更に 18O, 19O, 20O の計算にも成功したが,18F, 19F, 20Ne は成功しなかった.
この問題の解決は殻模型におけるa的4体相関の重要性を考慮することによって与えられた.19Fには何と110keVという低いエネルギーに1/2−という状態がある.これを説明するためにはどうしても0p1/2という負のパリティの閉殻軌道から1個粒子を正パリティの0d-1s軌道に上げなければならない.このために必要な励起エネルギーは,調和振動型平均場を仮定すると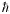 w〜12MeVは必要である.それがどうしてこのように低く出るか.その理由は1陽子が0pf1/2-軌道から励起して,0d-1s殻に入る.そこで0d-1s殻には2陽子-2中性子が入ることになり,20Neのように安定なa-クラスター的状態を作ることにあった.19Fの第1励起状態(1/2−)を用いて0p1/2孔と(0d-1s)4との相互作用を評価すると,きわめて弱いことが判る.そこで空孔と4粒子の弱結合近似を,有馬,堀内昶,瀬部孝は発表したのである.30)この着想を2空孔に拡張すると,まさに18Fの1.5MeVあたりに1+が現れて良いことが判明した.即ちこの状態は閉殻の励起を考えなければいけなかったのである.そしてエネルギーが低くなる理由はa-型相関のためであった.
w〜12MeVは必要である.それがどうしてこのように低く出るか.その理由は1陽子が0pf1/2-軌道から励起して,0d-1s殻に入る.そこで0d-1s殻には2陽子-2中性子が入ることになり,20Neのように安定なa-クラスター的状態を作ることにあった.19Fの第1励起状態(1/2−)を用いて0p1/2孔と(0d-1s)4との相互作用を評価すると,きわめて弱いことが判る.そこで空孔と4粒子の弱結合近似を,有馬,堀内昶,瀬部孝は発表したのである.30)この着想を2空孔に拡張すると,まさに18Fの1.5MeVあたりに1+が現れて良いことが判明した.即ちこの状態は閉殻の励起を考えなければいけなかったのである.そしてエネルギーが低くなる理由はa-型相関のためであった.
これに先立って,BrownとGreenは2重閉殻の16Oの第一励起0+状態が6MeVという異状に低いエネルギーに現れる理由を,当時の常識に大きく反して,閉殻より4核子が空殻に励起する.即ち4孔-4核子状態であると考えたのである.31)その原因として二人は16Oが励起すると大きく変形して,エネルギーを得するとしたのである.我々の弱結合近似を用いると,きわめて自然にその状態が6MeVに現れたのであった.即ちこの大きな変形はa-クラスター構造によることが明らかになった.
弱結合するのは何もa型4核子系の基底状態0+だけではなく,2+, 4+, 6+, 8+ という励起状態にも空孔が弱結合することが予想され,事実,Ogloblinたちの実験によって見事に証明されたのである.32)例えば19Fにはp−11/2と2+が結合した 3/2−, 5/2−, 4+ と結合した 7/2-, 9/2- などが存在している.
こうして空孔状態と思われるもの,例えば18Fの 1.5MeV 1+ を排除して0d5/2と1s1/2軌道のみを用いて,上述したArgonneのプログラムでx2-計算をすると,18O, 18F, 19O, 19F, 20Ne の構造を見事に説明できたのである.そして20Neの8+→6+遷移のB(E2)の予言値は後に行われた実験の測定値と見事に一致した.
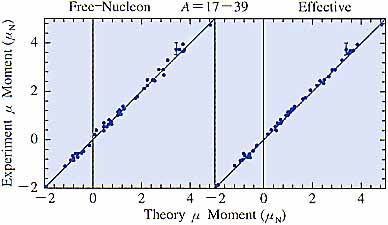
このような殻模型計算はその後も孜孜営営と続けられた.特にMSUの B. A. Brown とWildenthalの貢献は大きい.33)パラメタをx2-法で最適化して0d-1s殻の原子核すべてのエネルギー,磁気能率,g遷移,b遷移等々の計算に成功している.一例を挙げておこう(図7).
x2-法を40Caを越えた領域で用いて成功したのが,堀江久,小田健司,小川建吾のグループであった.現在でも (0f7/2, 0f5/2, 1p3/2, 1p1/2) 殻での計算の出発点になっている.34)
さて殻模型計算は計算機の進展と共に伸びてきた.その時最大の問題は,ハミルトニアンを対角化する際考慮に入れなければならない次元の大きさ,即ち基底の数である.例えば154Smは,Z=50, N=82 の2重閉殻の外に12個の陽子が50-82殻軌道に,10個の中性子が82-126殻軌道に入っている.この時の次元は
.gif)
等々である.1014次元の対角化をするのが大変であるが,その前に1014×1014の行列要素を勘定しなければならない.勿論実際0でない行列は,これよりずっと少ない.しかし,それにしても膨大な量の行列要素を計算しなければならないのである.
この問題を避ける二つの方法が考えられる.一つはその系が持つ何らかの対称性,例えば対相互作用に基づくシニオリティ形式(SU2対称性)とか,後述するElliottのSU3対称性などを用いて重要でないと考えられる状態を切り捨てること(truncation)である.この方法には一般に適切な対称性を見つけることがむずかしいという難点がある.もう一つは算法の工夫である.対角化をHouseholder法のように正面攻撃せず,低いもの(固有値の大きいもの)を何本か求めるLanczos法の応用ものそ一つであり,原子核には瀬部孝とNachamkin35)によって導入された.最近注目を浴びているのは Monte Carlo 法の応用であり,S. Koonin によって開発されている.36)この方法によると普通のやり方では達し得ない巨大な次元でも,計算可能になる.ただ計算の際に正の量であるべきものが負になるという問題が残っているし,最低エネルギー状態しか得られないという困難がある.そこで大塚孝治たちは出発点の状態を複数化し,Monte Carlo 法と対角化を組合せてこの困難を解決する可能性を提案している.37)
多粒子殻模型と近似的対称性
2体力が中心力のみでスピン軌道力がない時,LS結合方式が成立つ.ここでLは各粒子の軌道角運動量の和,Sはスピンの和である.このときLとSはそれぞれ良い量子数である.更に2体有効相互作用が,2核子の距離のみに依存するWigner力,距離と2核子の状態が座標の入れかえに対する対称性のみによるMajorana力の和である場合,全波動関数は空間対称性で分類できる.これをWignerの超多重項 (super multiplet) 理論という.38)軽い核で比較的良く成立する.*スピンだけからは19Ne(1/2+)→19F(1/2+)も19O(5/2+)→19F(5/2+)も許容b崩壊する筈であるが,前者は[3]対称から[3]対称で転移可能であるが,後者は19Oが [2, 1] に,一方19Fは[3]対称性に属しており,b崩壊の演算子はこの対称性を変えないから,19O→19Fのb崩壊は第1次近似では起らないことになる.事実後者の転移確率は小さい.
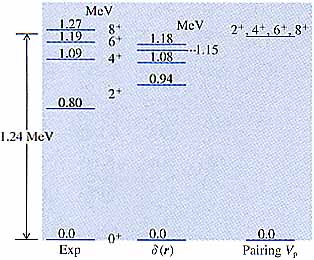
ZもNも偶数な原子核の基底状態のスピンは例外なく0+である.例えば208Pbに2中性子を加えると,この2個の中性子は1g9/2という軌道に入るから,全体の角運動量は 0+, 2+, 4+, 6+, 8+ が可能である.ここで 1+, 3+, 5+, 7+ はPauli禁止則によって禁止される.図8からわかるように0+が基底状態である.このことは2中性子間に0+や2+を低くする2体力が働いていることを意味している.この2体力の近似としてはd(r)型の引力を考えれば良い.もっと大胆に0+になるときだけ引力が働くと近似することもできる.このような力を単極-対相互作用と呼ぶ.j-軌道のみがあり,そこに多くの同種核子が入るとする.そして核子間にこの単極-対相互作用のみが働くと考えよう.その時
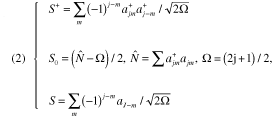
という三つの演算子を導入する.a+jmは粒子をjmの状態に生成,ajmはその状態から消滅させる演算子である.このとき単極-対相互作用は
![]()
と書ける.また S+, S0, S は
![]()
という交換関係を満足する.これはスピン演算子が満すものと全く同じである.そこでVpのみが働く系はSU2-群で分類できる.これをシニオリティ形式と呼び G. Racah が導入した.39)しかし上記のような演算子を用いると,この形式はSU2-群に他ならないことが明らかになった.そこで準スピン(quasi-spin)形式と言うこともある.準スピンの大きさは
![]()
である.この固有値をS(S+1)と書こう.また,j-軌道にいる陽子又は中性子をn個とすると,S0の固有値は(n−Ω)/2である.ただし2Ω=2j+1である.S+は0+-対(j2(0))を生成し,Sは0+-対を消滅する.n体系にSを何回か掛けて,これ以上0+-対を含まない状態を作り,それをjv(JM)とすると,このvをシニオリティと呼ぶ.このときS=(Ω−v)/2と書ける.また(4)によりVpの固有値は
![]()
で与えられる.重要なことはn体系jnでこの値を最低にするのは,gを負すなわちVpを引力として,nが偶数ならv=0のときであり,次に低いのはv=2のときである.そしてエネルギー差はgΩであり,これはv=0の2体系0+-対が持つエネルギーに他ならない.このgΩは超伝導のエネルギーギャップに対応する.nが奇数ならv=1が最低である.
Racah, Talmi, de Shalit はシニオリティ形式を大いに発展させたが,第2量子化を初期には用いなかった.40)従ってこの形式の理解はやや面倒であった.にもかかわらず,上記の事実を1950年当時の核理論研究者は良く知っていた.しかしこれを超伝導現象に結びつけて考える人は,私自身を含めていなかったことは残念である.上記の準スピンによる形式はBCS理論の発見に伴って,A. Kermanによって導入された.41)これはBCSで運動エネルギーを無視する強結合近似に対応し,和田靖,高野文彦,福田信之,Andersonによっても論じられた.42)また,原子核における超伝導性については Bohr, Mottelson, D. Pines によって指摘された.43)
準スピン形式による行列要素の計算などは Lawson, MacFarlane と独立に有馬と市村宗武によって発展された.44,45)ただし公式の殆どはRacahの導出したものであった.一つだけ長年の問題であったのはf(jnvJM)状態での,2体力の対角成分についての公式であった.これは古いやり方で有馬と河原田秀夫により46) 1964年に,1966年に準スピン形式で有馬--市村によって求められた.45)その公式は
.gif)
と書ける.F, G は n, v の2次関数である.n体系の行列要素がv体系のものに帰着することに注意して欲しい.ここで,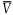 は粒子-空孔相互作用と呼ばれ,粒子-粒子相互作用から,粒子の一つを空孔へ変換することによって求まる.
は粒子-空孔相互作用と呼ばれ,粒子-粒子相互作用から,粒子の一つを空孔へ変換することによって求まる.
この公式によって一つの長年の問題が解決した.50Snのアイソトープで偶々核のエネルギー準位を見ると,基底状態は常に0+で,第1励起状態は常に2+である.しかもその励起エネルギーは殆ど一定である.一方,原子核構造の計算では良く単極-対相互作用とQ・Q相互作用の和が用いられる.ここでQは四重極能率(Q=r2Y(2)m(θ, j))である.後に述べる BCS+Random Phase Approximation の手法でしばしばこの力が用いられている.ところが対相互作用と,Q・Q相互作用のみでは2+の位置が粒子数nに大きく依存してしまうのである.そこでQ・Q力と2+-対のみにきく四重極-対相互作用を加えればnに依存しなくなることが,先程の公式から明らかになるのである.一般にV=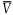 型の力であれば2+のエネルギーはnによらなくなるのである.これがQ・Q力に加えて四重極-対相互作用を必要とする一つの根拠になる.
型の力であれば2+のエネルギーはnによらなくなるのである.これがQ・Q力に加えて四重極-対相互作用を必要とする一つの根拠になる.
以上の準スピン形式は同一粒子のみの系で成立する.しかし現実には陽子と中性子がいる.j-殻に2種の核子が入り,単極-対相互作用があるときへの拡張は,市村宗武によって行われた.47)その時SU2ではなくO5群が必要になる.
SU(3)形式
Elliottは19Fの構造を多粒子殻模型で計算した.27)一方19Fの構造は,Bohr-Mottelsonの変形核模型にCoriolis力を考慮すると良く似た結果が得られることが知られていた.Elliottはそこで両者の間に密接な関係があると睨み,SU3模型を発見したのである.48)スピン軌道力を無視し調和振動子の平均場を仮定する.さらにQ・Q力のみが働くとすると,この力はSU3形式で対角的である.そのエネルギーは
![]()
で与えられる.ここでC(lm)はSU3群のCasimir演算子,lmは表現のラベルである.この式で自然に回転エネルギーが得られることが判る.またQ0=(3z2−r2)はC(lm)とは交換し,同時対角化できる.これはBohr-Mottelson模型のintrinsic状態に対応する.ただしLの固有状態を射出 (project out) しなければならない.
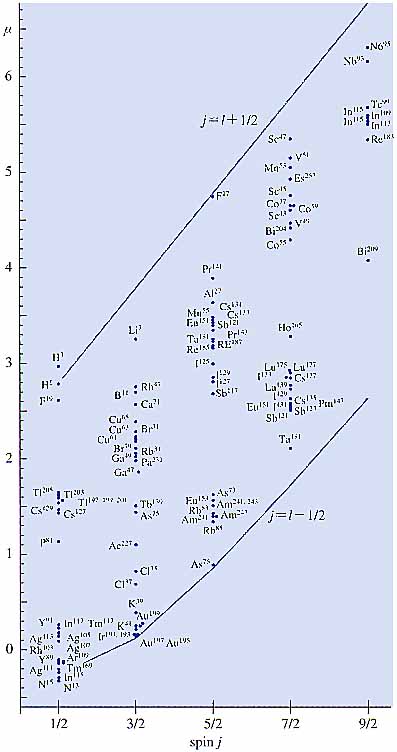
SU3-形式の良い応用は0d-1s核であり,特に20Neである.秋山佳己,有馬,井上健男,瀬部孝をはじめ,SU3群を用いて状態を制限した多くの計算がある.49)しかし先述したように現在は完全に対角化が行われるようになったので,このような制限法は不要になったかも知れない.しかし殻模型と回転運動及びすぐ後で述べるクラスター模型との関係を見る上で,SU(3)模型は今でも役立っているのである.
|
|
図5 奇陽子核の磁気能率のSchmidt図. |
|
|
図6 20Neのスペクトル.殻模型による予言と実験. |
|
|
図7 0s-1d殻の磁気能率.実験値と殻模型による予言値. |
|
|
図8 210Pbのエネルギー準位. |
3. クラスター模型
原子核でクラスターとは,核内で中性子や陽子のみでなく,重陽子や3重水素,3He, 4He=aなどやそれに近い状態を作っているとき,このような成分をいう.核がいくつかのクラスターからできているという考えは,早くも1937年にWheelerにより共鳴群模型として提案されたが,計算が困難なため長年用いられなあった.50)この模型はドイツのHackenbroichグループ,ロシアのNeudatchinグループなどがp-殻に応用していた.51)またWildermuthとKanellopoulosは各クラスターが調和振動子の単一粒子からなるとし,相対運動もまた調和振動子という模型を出した.52)しかし直ちにBaymanとBohrによってこれはSU3結合と同一であると批判された53)ために,この方向はあまり発展しなかった.
最も精力的にこのクラスター模型を発展させたのは日本である.出発点は1960年代に田中一,玉垣良三を中心にした共鳴群法に基づくaとaの散乱の分析であった.54)この計算によって2a間の近距離での斥力の起源が核子間のPauli禁止則に原因があることが明らかになった.そして一般にPauli禁止則のためクラスター間相対運動がとれないPauli禁止状態の概念が生み出された.それに基づきクラスター間相対運動を記述する強力な模型として,直交条件模型が斉藤栄により提案された.55)
先述したように20Neは殻模型でも良く理解できる.しかしまた,この状態は16O+aとすることもできる.ただし(0d-1s)4では8+までしか発生しないし,実験的にもそうである.一方,クラスター模型に殻効果を入れなければいけないことが明らかである.このような混合模型に基づく計算は例えば友田敏章によって行われた.56)ここで16Oとaとは相互作用が弱いこと,(0d-1s)4のa的状態と0p-孔とが弱結合している,というような事実から堀内昶と池田清美は,20Neが単に殻模型の枠内で4粒子が強く相関するだけでなく,空間的にクラスターが局所的に存在し,16O+a構造を持つなら正パリティ回転状態以外に,それとパリティ2重項の関係にある負パリティ回転状態が存在することを予想した.そして16O+a弾性散乱の共鳴準位として見つかった負パリティ回転帯をそれと同定し,殻模型的平均場内のクラスター相関の研究の他に,空間的に局在するクラスター構造の研究へ向う端緒を作ったのである.57)
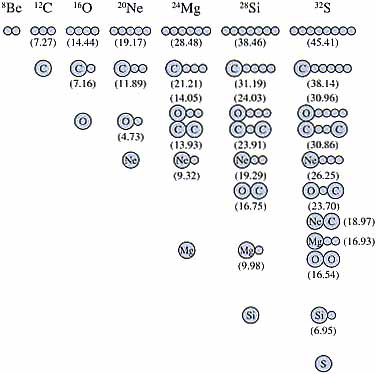
16Oには 6.0MeV 0+ を起点とする(0p)−4−(0d-1s)4型の20Neに似た回転帯があることは,先述した弱結合近似の予言通りである.これも20Neの基底状態もそれぞれa粒子分離の閾値エネルギー近傍にある.また森永晴彦が三つのa粒子が鎖状に連なる構造を持つと推定した12Cの正パリティの励起状態もまた,a粒子分離の閾値エネルギー近傍に存在する.58)このようにクラスター的状態はお互いに弱い相互作用をするようなエネルギーに発現する.強ければ融合して殻模型的構造になってしまうであろう.従ってクラスター状態はクラスター分離の閾値付近に現われる筈である.これを閾値則と呼ぶ.それに基づいて発現が期待されるクラスター分子的構造を図式で表現したものを池田図と呼んでいる.
殻模型的構造と共存し,またそれに結合するクラスター構造の研究を進めるには,微視的に核子の自由度まで戻ったクラスター模型を開発しなければならない.その代表的手法は上述したWheelerの共鳴群法であるが,極めて煩雑で実際計算できるのは0p殻前半の核に限られていた.一方同じくWheelerによって提案された生成座標法は,集団運動を記述する上で有力であり,しかも計算が容易である.59)そこで堀内昶は,D. Brink が導入したSlater行列型のクラスター模型波動関数を用いた生成座標法と,共鳴群法とは等価であることを証明し,両方法の間の交換公式を導いた.60)こうして計算が遙かに易しい生成座標法の積分核から,この交換公式により共鳴群法の積分核が計算できるようになったのである.上村正康は広がりパラメタの異なるガウス関数を単一粒子を記述するのに用い,上記の変換を使って,原子核(それ自身一つのクラスター)間の散乱を取り扱う計算法を大幅に発展させたのである.61)そして実験をまさにきわめて正確に予言するに到った.
クラスター模型は特に軽い核で有効である.最近不安定核を加速することによって,中性子や陽子の放出限界に近いところまで新しい不安定核の研究が進んでいる.その中でも谷畑勇夫を中心にした11Li,特にその,いわゆる中性子ハローの発見は重要であった.62)このような核の研究にもクラスター模型は有力である.
クラスター模型の研究に関係して,分子共鳴状態の問題と重い核のa崩壊の問題がある.分子共鳴の理論的研究は1960年代の実験に触発されて,野上茂吉郎と今西文龍によって始められた.63)その発展としてバンド交叉模型が阿部恭久たちによって提唱され多くの成果を上げている.64)一方重い核のa崩壊に関しては H. Mang による先駆的研究が殻模型を用いて行われた.原田はその絶対値が単極-対相互作用により大きく増幅されることを示した.65)しかし依然絶対値は実験に比べて遙かに小さかった.殿塚勲と有馬は殻模型波動関数に高エネルギー配位を系統的に混合することにより,親核の核表面のクラスター形成確率が著しく増大することを,212Po→208Pb+aを例にとり調べた.66)この流れの上の最近の仕事にVargaたちの仕事がある.67)またa崩壊に関して,表面近くのaの娘核に対する相対運動について,Pauli禁止則の影響を入れて規格化しなおすべきであることが,Fliessbachによって指摘された.68)この効果は20Ne→16O+aで指摘されたが,上村正康,松瀬丈浩,福嶋義博の計算でも知られていたことであり,65)有馬朗人と吉田思郎の20Neのa崩壊の計算は規格化しなおす必要があったのである.70)しかし依然として核内と核外のa-クラスター波動関数を重い核でどうつなぐかは問題である.なお対相関によって2核子転移確率が著しく増幅されることは1961年吉田思郎によって予言され,実験で確かめられている.71)原子核における超伝導性の確立の上で大きな仕事であった.
|
| 図9 池田図.原子核がa粒子を構成単位とするサブユノットへこわれる閾値エネルギーを図示したもの.この閾値付近にサブユニットに対応する分子的構造が現れ易いと考えられている. |
4. 原子核の集団運動
乱雑位相近似(RPA)
1953年BohrとMottelsonは核の液滴模型をとり,表面振動を量子化した.72)この表面振動模型が核の低エネルギー準位に関する数多くの実験事実を説明した.そこで個々の核子の運動から表面振動を理解しようという努力が始まった.勿論変形核とその回転運動についても同様である.後者については日本では朝永振一郎の仕事があるが,残念ながら発展が見られていない.73)宇井治生,最近では D. Rowe と共同研究者が,いわばElliottのSU3をnon-compact群へ拡張した SU(1,1) 模型を提案したが,ある意味で朝永模型の発展という側面を持っている.74)
表面振動は,物性論におけるプラズマ現象について成功した.沢田達郎による乱雑位相近似 (Random Phase Approximation, RPA) を原子核に適用して,素励起モードを説明しようという試みがなされた.75)高木修一による3−振動,76)田村太郎,宇田川猛による2+振動などがその先駆的なものである.77)
2+を1表面振動子(ボソン)の励起とし,2個振動子を励起させると 0+, 2+, 4+ という三つの状態が生じ,第1励起エネルギーの2倍のところに現われる筈である.その傾向はあるが,三つの状態のエネルギーはかなり違っている.これは非調和効果と呼ばれる.また,本来のフェルミオン系から,振動子というボソンをどうして作るかが問題になる.そこでフェルミオン多体系からボソン多体系の写像を導入する考えがある.これを最初にやったのは1962年のBelyaevとZelevinskyであった.78)彼らはフェルミオン演算子をボソンのものと置きかえようとしたのである.これに対して丸森寿夫,山村正俊,徳永旻は,二つの異なる空間での行列要素が等しくなるような写像を行おうという方法を提案した.79)丸森グループの活躍は日本の集団運動研究の発展を促した.80)例えば岸本照夫,田村太郎によるボソン展開法,81)高田健二郎らによるDyson型ボソン展開法などはその発展の線上にある.82)最近の発展としては,集団運動部分空間を微視的な立場から規定する方法として,自己無撞着集団座標法が,丸森寿夫,益川敏英,坂田文彦,栗山惇により提案されている.83)これらの模型では閉殻の場合を除き,殆どすべてまずBCS近似で単極-対相互作用を処理し,BCS真空の上に準粒子-準粒子の対で素励起状態を作っている.これがすぐ後で論じる相互作用するボソン模型での2核子対と密接な関係があることが判っている.
相互作用するボソン模型
有馬は1966年に相互作用するボソン模型の雛型となるものを提案していたが,84) 1974年 F. Iachello と協力して「相互作用するボソン模型(IBM)」を打出した.85) IBMではスピンのパリティが0+と2+のsボソンとdボソンを仮定する.sボソンの数をNs,dボソンの数をNdとすると,全ボソン数N=Ns+Ndが保存されると考える.次にIBMのハミルトニアンは,ボソンの1粒子エネルギーと2体のボソン-ボソン相互作用からできていると仮定する.相互作用の強度を示すパラメタの値を適切に選ぶと,さまざまな偶々核の励起エネルギーや転移確率を良く説明できる.核力という複雑で強い相互作用を通じて束縛されている多核子であるという事実からは,想像もつかないほど美しい規則性があることが発見された.この模型の基礎になる対称性はSU(6)群である.
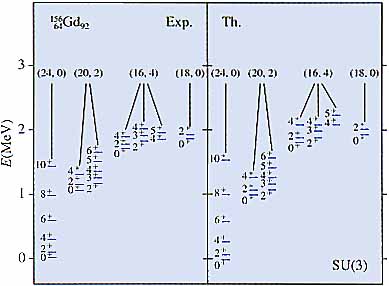
IBMのボソン・ハミルトニアンは6個の独立なパラメタを含む.それが適当な値をとるとき,三つの極限的な場合が得られ,そのときハミルトニアンを解析的に解くことができる.これは(1)球形核表面の四重極振動(振動核),(2)楕円体変形の回転(回転核),(3)軸の長さが振動しながらの回転(ガンマ不安定核)に対応している.IBMではそれぞれ O(5), SU(3), O(6) 極限と呼んでいる.なお(1)の場合,先述した非調和性は自然に考慮されている.この典型的な場合のエネルギー準位の実験との比較を図10に示しておく.
IBMの微視的基礎づけが次の問題であった.その時最も有力な考え方は,ボソンをコヒーレントな核子対に対応させるものである.まず原子核のBCS状態をつくる 0+ Cooper 対(S対と呼ぶ)に対してsボソンを,このコヒーレント対を2+に拡張したもの(D対)に対してdボソンを対応させる.閉殻外軌道にいる核子の個数nが縮退度Ω=S(2j+1)/2に比べて小さければ,これらの核子対はボソン的振舞をする.しかしnは2Ωを超えられない.これがボソンの数をIBMでは保存させる理由である.
フェルミオンよりボソンへの写像は,両空間で行列要素が等しいことを要請するOAI写像が良く用いられている.86)これは丸森写像と精神において共通する所がある.この方法は振動核や遷移核ではうまくいっているが,変形核においてはいまだに問題がある.この事実は吉永尚孝によって詳しく調べられている.87)
IBMの拡張として中性子と陽子それぞれに対して s, d ボソンを導入するnp-IBM (IMB-2) や,奇A核を記述するためフェルミオンを加えたIBFMなどが成功を収めている.88,89)
原子核の高い励起状態の集団運動的性質の研究は1963年の森永晴彦とGugelotの (a, nx) の仕事が始まりであった.90)また偶々核の回転帯及び振動運動についてのきわめて包括的情報の整理が坂井光夫によって精力的に行われた.91)私たちの理論的研究はこの3人の実験家の業績に大きく依存しているのである.
核力と有効相互作用
原子核の構造を理解するために最も基本的なことは,核子間の相互作用即ち核力である.核力の研究は湯川秀樹の中間子論(1935年)に始まり,92)日本グループが中心的役割を演じた.武谷三男は1956年に,核力をその到達距離によって三つの領域に分けて研究を進めることを提案し,大きな影響を与えた.三つの領域とは,(I) 2 fm 以上離れて静的な1パイオン交換による核力(OPEP)がきく領域,(II) 1〜2 fm で,パイオン交換の非静的部分や,2個以上のパイオン交換,重い中間子の交換などが寄与する領域,(III) 1 fm より近距離で,複雑な相互作用がある領域,である.
この考えに従って領域(I)でOPEPが岩垂純二たちによって1956年に確立した.93)領域(II)では福田-沢田-武谷により非静的パイオン-核子相互作用が定式化され,武谷-町田-大沼ポテンシャルが提案された.94)領域(III)では強い斥力があることが判ってきている.
この強い斥力をハード・コアで近似する浜田-Johnstonポテンシャルと,有限な斥力(ソフト・コア)で近似するReidポテンシャルが導入された.95)どちらもパラメタが核子-核子散乱のデータに合せてあり,現象論的ではあるが,核構造や核反応計算の基礎的ポテンシャルとして長く用いられた.
1970年以後領域(II)の研究が進んだが,それは主としてフランスやドイツで行われ,日本の伝統は失われたかに見えた.
しかし領域(III)の斥力を理解する上で日本のグループはその伝統を復活した.まずa-a散乱から類推して核子のクォーク構造とクォークの反対称化から生じる斥力の可能性である.それを最初に指摘したのは V. G. Neudatchin, Y. F. Smirnov と玉垣良三であり,1977年であった.96)しかしそれだけではなくクォーク間力まで考慮に入れなければならないことが岡真と矢崎紘一によって示された.97)その際クォークは非相対論的に取扱い共鳴群法を用いて計算している.こうして近距離斥力の起源がかなり明確になったのである.更にSU(3)クォーク模型による短距離力,クォーク・クラスター模型による短距離力と中間子力を組合せて核力のみならず一般のバリオン間相互作用を導出する試みなどが行われている.
少数多体系と有効相互作用の理論
前項で論じた核力で核構造を論じるのが理想的であるが近距離の斥力―特にハード・コア―があるため摂動計算が使えないという困難がある.
しかし3体系では核力から出発して厳密に計算することが可能になった.1980年代に入ってからである.それはFaddeev方程式を精度良く解くことができるようになったからである.この3体問題では笹川辰弥とその協力者が大いに活躍している.98)またHannoverグループと Los Alamos グループの寄与も大きい.トリトンの結合エネルギーはReidポテンシャルで 7.35MeV, Argonne V14 ポテンシャルで7.67MeVとなる.実験値8.45MeVには少々足りない.そこで現象論的な3体力を加えて結合エネルギーに合わせると,形状因子,Coulombエネルギー等の性質を良く再現することができる.
変分法も用いて3体以外の軽い核についてもかなり精度が良い計算が行われていて,4Heの場合,その結合エネルギーは前述のReidポテンシャルで 23.5MeV, Argonne V14 ポテンシャルで24.6MeVである.実験は28.3MeVであるが,この差は3Hの束縛エネルギーで必要であった3体力で説明できることが知られている.99)このような性質が非相対論的取扱いで再現できることは注意すべきである.
有効相互作用
もっと質量が大きくなったとき,強い近距離斥力を考慮に入れるには,変分関数にII f(rij)という関数を掛ける方法がJastrowによって提案された.100)ここでf(r)はrが小さくなると0になり,遠くなると1になる関数である.この方法は岩本文明と山田勝美によって発展させられた.101)有限核ではあまり使われなかったが,最近4Heより少し重い核で用いられている.しかし大計算になるために普通はBruecknerのG行列理論とそれを発展させたBethe-Goldstone方程式を解くことから出発する.102, 103)こうやって求めたG行列を用い,芯偏極効果など高次の補正を加えて殻模型に用いる有効相互作用を計算することも行われている.特にKuoとBrownによって精力的に計算が進められた.104)日本でも坂東弘治,永田忍たちを中心とする京都グループの寄与が大きい.105)
1982年鈴木賢二は,ユニタリー模型―演算子法を提案したが,これによって現実的な2体核力からG行列を求め,それから使用可能な有効相互作用を求める,一つの処方が得られたと言えそうである.事実,鈴木と岡本良治が16Oに応用した結果は有望である.106)
Brueckner-Betheの方法で得られたG行列を用いてHartree-Fock計算が多数行われた.しかし核物質の結合エネルギーと密度の実験値を得るに到っていない.
近年Waleckaによって相対論的平均場近似が導入された.107)この模型に基づいてHartree-Fock計算をすると,核物質の性質が良く説明できるという.しかし手離しで喜べない.軽い核では相対論効果なしで説明できたのに,16Oぐらいになるとどうして相対論効果がいるようになるのか,不思議である.また核子はクォークからできている.それがかたまって核子になって,核子全体としてはDirac方程式を満たすようになるのは,どのような仕掛によるのであろうか.
巨大共鳴
原子核がg線を吸収すると励起エネルギーが77A−1/3MeVあたりに大きな確率で励起する.これは電気双極子遷移によるものであり,遷移確率は古典的和則をほぼ満たしている.これをE1巨大共鳴と呼ぶ.
原子核が変形すると長軸方向のE1巨大共鳴と短軸方向のものとは違ってくる筈である.この可能性は岡本和人とDanosによって指摘された.108)実験により確められている.
E2巨大共鳴やE0巨大共鳴の存在は以前から指摘されていたが,その発見には鳥塚賀治を中心とする東北大グループの寄与が大きい.109)
スピンに関する巨大共鳴としては,アイソバリック・アナログ状態の発見の直後,藤田純一,藤井三朗と池田清美によってGamow-Teller巨大共鳴が1963年に予言された.110)この状態は1975年Indianaグループの(p,n)反応によって発見された.111) LS結合が成立する軽い核だと,空間対称性即ちWignerの超多重項が良い近似であり,そこではアナグロ状態だけではなく,G-T状態も当然存在する.しかしスピン-軌道力もCoulomb力も大きい,従って空間対称性がきわめて破れている中重核や,重い核に,アナグロ状態もG-T状態も存在するという事実は,驚きをもって迎えられた.
ところで,このG-T状態の(p, n)反応断面積は,殻模型による理論値の1/3ぐらいしか実験的に発見されていなかった.そこでD-空孔状態が混って(p,n)反応の断面積を小さくする可能性が指摘された.一方,浜本とBertschは,G-T状態に2粒子-2空孔状態が混ることによって,この断面積が小さくなることを指摘した.112)これは有馬,市村,清水が主張したテンソル相関に他ならない.2粒子-2空孔が基底状態に混ることは,逆にG-T状態が沢山ある2粒子-2空孔状態に混ることを意味する.そこで2粒子-2空孔が分布する40〜50MeVの励起状態への(p, n)反応の断面積を測って和をとれば,予想される和則を満足する筈である.こういう説が浜本たちや有馬たちのものである.もしD-空孔の混合が本当に必要であれば,和則を満足するためにはDの励起エネルギー300MeV前後まで和をとる必要があることになる.実験が軍配をどちらへ上げるであろうか.私はテンソル相関の重要性が実験で既に以下のように確かめられていると思う.
Dのアイソスピンは3/2,1空孔のものは1/2であるから,D-h状態のアイソスピンは1か2である.そこでアイソスピンが1だけ変る遷移には,D-hの混合がきく可能性があるが,アイソスピンが変らない遷移ではD-hはきかない.しかし実験的にはアイソスピンが変化しないような(DT=0)励起も,断面積が抑制され小さいことが判っている.また2個の鏡映核(例えば178O9と179O8)の磁気能率の和の1/2,すなわちアイソスカラー磁気能率のスピン部分が,殻模型値よりずっと小さいことが確かめられた.アイソスカラーな量にD-空孔の影響は第1次近似で0である.しかしテンソル相関はこの場合にも大きな効果を持ち,実験値を良く説明できる.113)
アイソベクトル型の遷移でD-空孔の効果が大きく評価され過ぎたのは,軽い核については表面効果が無視されたこと,中重核では残留相互の近似としてよく用いられるLandau-Migdal力を大きくとり過ぎたためである.2倍にして入れたという計算間違いの論文は論外にしても,全卓樹と清水清孝が指摘したようにもう少し小さい値をとるべきである.114)そうするとLandau-Migdal力を用いないでやった計算,例えばTownerとKhannaの結果とも良く一致する.115)
E1やE2巨大共鳴の幅には,共鳴の主要部分である1粒子-1空孔状態が直接に粒子を放出する幅と,1粒子-1空孔が2粒子-2空孔以上の複雑な状態に移っていく幅がある.前者を崩壊幅,後者を分散幅と呼ぶ.後者について16Oと40Caをとって最もきちんとした計算が星野享と有馬によって,116)又中重核や重い核でも用いられる普遍的な優れた計算法が吉田思郎と安達静子によって提案された.今日世界的に類似の方法が用いられているが,吉田-安達を出発点としていると言ってよい.117)
素粒子のY-scalingの概念を原子核のE1巨大共鳴に応用して,武田暁と川添良幸はこの概念が原子核でも良く成立つことを示した.118) Westも同じ結論を前後して得ている.119)このようなscalingとか,総和則とかは,しばしば問題にしている体系の大局的な性質を調べる上で,大変役に立つ.このY-scalingはその良い例と言えるのである.
ハイパー核の構造
素粒子のSU(3)模型によれば,陽子,中性子と6個のハイペロン (Λ, S+, S0, S−, X0, X−) は一つの組を作っていて脂質が良く似ている.ただしハイペロンはストレンジネスを持っていて,質量が核子より少々大きい.このハイペロンが含まれている核をハイパー核と呼んでいる.ハイパー核の研究は原子核構造研究の先端の一つである.
この分野における故坂東弘治を中心としたグループの活躍は,GalやDoverに互して大きなものである.特に山本安夫と坂東はバリオン間相互作用から出発し,ハイペロンと核子間のG行列を作ったところが特筆すべきである.120)この行列を用いてハイペロンの核内での単一粒子運動の性質を導いている.例えば平均場の形や深さ,有効質量,スピン-軌道力である.こうして得られた核子-ハイペロン有効相互作用を用いた殻模型計算は元場俊雄,糸永一憲たちによって精力的に進められている.また日本で特に開発が進んでいるクラスター模型のハイパー核への応用も活発に行われている.この方法で軽いハイパー核の生成,構造,崩壊がかなり良く理解されている.
原田融や赤石義紀たちはS粒子と原子核相互作用を研究し,Sハイパー核の可能性を検討した.Sの寿命は短いのみならず核子と強い相互作用をするので,幅の狭いSハイパー核が存在するかどうか疑問である.しかし赤石たちは4SHeの存在を予言し,121)事実早野龍五たちの KEK, BNL での実験によって実証されたのである.122)
温度の高い変形核及び超変形核
変形核については Hartree-Fock-Bogoljubov (HFB) 法を用いた研究が標準的である.ここではつじつまの合った平均場を生み出すためにHF法が用いられ,その上に強い単極-対相互作用の効果を加味するため,Bogoljubov変換が考慮に入れられている.近年変形核の高いエネルギーの研究が盛んになり,レベル単位の密度や変形が温度とともにどう変化するかが問題になってきている.この場合HFB法に温度の効果を考えに入れなければならない.そのような計算において田辺孝哉及び菅原・田辺和子の活躍は注目すべきである.123)
長軸と短軸の比が2:1になるような大きな変形核の存在は,核分裂アイソマーの発見によって明らかになったが,そのような大きな変形核が持つ回転状態の研究が大いに発展した.この超変形核の回転帯の発見は最近の原子核物理学における最も重要な事項の一つである.
色々面白い性質が見つかっているが,その一つは,一つの偶々核とその隣の奇核が全く同じ回転帯を持つことである.浜本育子とMottelsonの擬スピンによる説明がある.124)ここで擬スピン機構は有馬,清水,Harveyにより,125)また独立にHechtたちによって発見された.126)殻模型の軌道で,例えばp3/2と f5/2, f7/2 とh9/2のように,(l, j=l+1/2) と (l+2, j´=l+2−1/2) の2本の軌道のエネルギーがほぼ縮退している.そこで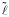 =l+1という擬角運動量を導入すると (
=l+1という擬角運動量を導入すると (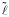 , j=
, j=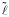 −1/2), (
−1/2), (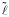 , j´=
, j´=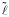 +1/2) と読み換えることができる.このlと擬スピンsを用いると,擬スピン・軌道力(
+1/2) と読み換えることができる.このlと擬スピンsを用いると,擬スピン・軌道力(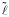 ・s)が殆ど0ということになる.そこで擬スピンを用いると,
・s)が殆ど0ということになる.そこで擬スピンを用いると,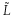 =S
=S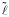 iと
iと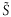 −S
−S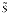 iがどちらも良い量子数を与えるのである.
iがどちらも良い量子数を与えるのである.
このような超変形核でクランクト殻模型がよく使われるが,これにRPAを加えた興味深い研究が松柳研一たちによって行われている.127)この分野は実験的にも理論的にも更に大きな発展が期待される.
最後に中間エネルギー核物理の発展について述べるべきであるが,予定の枚数を遙かに上廻ったので割愛することをお許しいただきたい.
この論を書くに当って矢崎紘一,大塚孝治,堀内昶,岡真,吉永尚孝,全卓樹の諸氏と小川洋子さんのご援助をいただいた.ここに深く感謝する.
|
|
図10 156Gdのスペクトル.実験値とIBMとSU(3)極限による予言値.(二つのパラメータを実験に合せてある.) |
参考文献
- C. F. von Weizsacker: Z. Phys. 96 (1935) 431. H. A. Bethe and R. F. Bacher: Rev. Mod. Phys. 8 (1936) 82.
- O. Hahn and F. Strassman: Naturwissenschaften 27 (1939) 11.
- N. Bohr and J. Wheeler: Phys. Rev. 56 (1939) 426.
- E. P. Wigner: Phys. Rev. 51 (1937) 106.
- M. G. Mayer and J. H. D. Jensen: Elementary Theory of Nuclear Shell Structure (Wiley, New York, 1955).
- J. Rainwater: Phys. Rev. 79 (1950) 432; Rev. Mod. Phys. 48 (1976) 385.
- A. Bohr: Mat. Fys. Medd. Dan. Vid. Selsk. 26 (1952) No. 14; Rotational States of Atomic Nuclei (Munksgaard, Copenhagen, 1954). A Bohr and B. R. Mottelson: Nuclear Structure, Vol. 2 (Benjamin, New York, 1975).
- S. G. Nilsson: Mat. Fys. Medd. Dan. Vid. Selsk. 25 (1955) No. 16.
- H. Miyazawa: Prog. Theor. Phys. 6 (1951) 801.
- T. Yamazaki, T. Nomura, S. Nagamiya and T. Katou: Phys. Rev. Lett. 25 (1970) 547. S. Nagamiya and T. Yamazaki: Phys. Rev. C 4 (1971) 1961.
- A. Arima and H. Horie: Prog. Theor. Phys. 11 (1954) 509. A. Arima and H. Horie: ibid. 12 (1954) 623.
- R. J. Blin-Stoyle: Proc. Phys. Soc. A 66 (1953) 1158. R. J. Blin-Stoyle and M. A. Perks: ibid. A 67 (1954) 885.
- M. Chemtob: Nucl. Phys. A 123 (1969) 449.
- H. Hyuga and A. Arima: Proc. Int. Conf. Nuclear Moments and Nuclear Structure, Osaka, 1972, J. Phys. Soc. Japan 34 (1973) Suppl., p. 538.
- I. S. Towner and F. C. Khanna: Nucl. Phys. A 399 (1983) 334; Phys. Rev. Lett. 42 (1979) 51.
- K. Shimizu, M. Ichimura and A. Arima: Nucl. Phys. A 226 (1974) 282.
- J. I. Fujita and H. Hirata: Phys. Lett. 37B(1971) 237.
- A. Arima, G. E. Brown, H. Hyuga and M. Ichimura: Nucl. Phys. A 205 (1973) 27.
- H. Horie and A. Arima: Phys. Rev. 99 (1955) 778.
- M. J. Stevenson and C. H. Townes: Phys. Rev. 107 (1957) 635.
- R. D. Amado: Phys. Rev. 111 (1958) 548.
- B. R. Mottelson: Le Prix Nobel, en 1971〜en 1976, by the Nobel Foundation [邦訳:ノーベル賞講演物理学12,中村誠太郎・小沼通二編1973〜1976(講談社)].
- A. Arima, H. Horie and M. Sano: Prog. Theor. Phys. 17 (1957) 567.
- A. Arima and H. Horie: Proc. Rehovoth Conf. Nuclear Structure, ed. H. J. Lipkin (Weizmann Institute, Rehovoth, 1957) p. 213.
- I. Hamamoto: Nucl. Phys. 62 (1965) 49, 66 (1965) 176.
- D. R. Inglis: Rev. Mod. Phys. 25 (1953) 390.
- J. P. Elliott and B. H. Flowers: Proc. Roy. Soc. (London) A 229 (1955) 536.
- T. Inoue, T. Sebe, H. Hagiwara and A. Arima: Nucl. Phys. 59 (1964) 1.
- S. Cohen, R. D. Lawson, M. H. MacFarlane and M. Soga: Phys. Lett. 9 (1964) 180.
- A. Arima, H. Horiuchi and T. Sebe: Phys. Lett. 24B (1967) 129.
- G. E. Brown and A. M. Green: Nucl. Phys. 75 (1966) 401.
- V. V. Davydov, A. A. Ogloblin, S. B. Sakuta and V. I. Chuev: Izv. Akad. Nauk SSSR, Ser. Fiz. 33 (1969) 597 [Bull. Acad. Sci. USSR, Phys. Ser. 33 (1970) 551]. Y. A. Glukhov, B. G. Novaskii, A. A. Ogloblin, S. B. Sakuta and D. N. Stepanov: Izv. Akad. Nauk SSSR, Ser. Fiz. 33 (1969) 609 [Bull. Acad. Sci. USSR, Phys. Ser. 33 (1970) 561]. V. Z. Goldberg, V. V. Davydov, A. A. Ogloblin, S. B. Sakuta and V. I. Chuev: Izv. Akad. Nauk SSSR, Ser. Fiz. 33 (1969) 566 [Bull. Acad. Sci. USSR, Phys. Ser. 33 (1970) 525].
- B. A. Brown and B. H. Wildenthal: Annu. Rev. Nucl. Part. Sci. 38 (1988) 29-66.
- H. Horie and K. Ogawa: Prog. Theor. Phys. 46 (1971) 439. H. Horie and T. Oda: Prog. Theor. Phys. Suppl. Extra No. (1968) 403.
- T. Sebe and J. Nachamkin: Ann. Phys. 51 (1969) 100.
- S. E. Koonin: Nucl. Phys. A 574 (1994) No. 1-2, 1-9. C. W. Johnson, S. E. Koonin, G. H. Lang and W. E. Ormand: Phys. Rev. Lett. 69 (1992) 3157.
- M. Honma, T. Mizusaki and T. Otsuka: Phys. Rev. Lett. 75 (1995) 1284.
- E. P. Wigner: Phys. Rev. 51 (1937) 106.
- G. Racah: Phys. Rev. 63 (1943) 367.
- A. De Shalit and I. Talmi: Nuclear Shell Structure (Academic, New York, 1963).
- A. K. Kerman: Ann. Phys. (USA) 12 (1961) 300.
- P. W. Anderson: Phys. Rev. 112 (1958) 1900.
- A. Bohr, B. R. Mottelson and D. Pines: Phys. Rev. 111 (1958) 936.
- A. K. Kerman, R. D. Lawson and M. H. MacFarlane: Phys. Rev. 124 (1961) 162.
- A. Arima and M. Ichimura: Prog. Theor. Phys. 36 (1966) 296.
- A. Arima and H. Kawarada: J. Phys. Soc. Ipn. 19 (1964) 1768.
- M. Ichimura: Nucl. Phys. A 131 (1969) 398.
- J. P. Elliott: Proc. Roy. Soc. London A 245 (1958) 128, 562.
- Y. Akiyama, A. Arima and T. Sebe: Nucl. Phys. A 138 (1969) 273. N. Yoshinaga, Y. Akiyama and A. Arima: Phys. Rev. C 38 (1988) 419; Phys. Rev. Lett. 56 (1986) 1116.
- J. A. Wheeler: Phys. Rev. 52 (1937) 1083, 1107.
- H. H. Hackenbroich: Z. Phys. 231 (1970) 216. H. H. Hackenbroich and P. Heiss: ibid. 225. H. Hutzelmeyer and H. H. Hackenbroich: ibid. 232 (1970) 356. H. H. Hackenbroich, T. H. Seligman and W. Zahn: Nucl. Phys. A 259 (1976) 445. V. G. Neudatchin and Yu. F. Simirnov: At. Energy Rev., 3 (1965) 157; Prog. Nucl. Phys. 10 (1969) 275.
- K. Wildermuth and Th. Kanellopoulos: Nucl. Phys. 7 (1958) 150, 9 (1958/59) 449.
- B. F. Bayman and A. Bohr: Nucl. Phys. 9 (1958/59) 596.
- R. Tamagaki and H. Tanaka: Prog. Theor. Phys. 34 (1965) 191. I. Shimodaya, R. Tamagali and H. Tanaka: ibid. 27 (1962) 793. J. Hiura and I. Shimodaya: ibid. 30 (1963) 585, 36 (1966) 977.
- S. Saito: Prog. Theor. Phys. 40 (1968) 893, 41 (1969) 705.
- T. Tomoda and A. Arima: Nucl. Phys. A 303 (1978) 217.
- K. Ikeda, N. Takigawa and H. Horiuchi: Prog. Theor. Phys. Suppl. Extra No. (1968) 464. H. Horiuchi, K. Ikeda and Y. Suzuki: ibid. Suppl. No. 52 (1972) Chap. 3.
- H. Morinaga: Phys. Rev. 101 (1956) 254.
- D. L. Hill and J. A. Wheeler: Phys. Rev. 89 (1953) 1102. J. J. Griffn and J. A. Wheeler: ibid. 108 (1957) 311.
- H. Horiuchi: Prog. Theor. Phys. 43 (1970) 375.
- M. Kamimura: Prog. Theor. Phys. Suppl. No. 62 (1977) 236.
- I. Tanihata, H. Hamagaki, O. Hashimoto, Y. Shida, N. Yoshikawa, K. Sugimoto, O. Yamakawa, T. Kobayashi and N. Takahashi: Phys. Rev. Lett. 55 (1985) 2676. T. Kobayashi, O. Yamakawa, K. Omata, K. Sugimoto, T. Shimoda, N. Takahashi and I. Tanihata: ibid. 60 (1988) 2599. P. G. Hansen and B. Jonson: Europhys. Lett. 4 (1987) 409.
- B. Imanishi: Phys. Lett. 27B (1968) 267; Nucl. Phys. A 125 (1969) 33.
- K. Kato, S. Okabe and Y. Abe: Prog. Theor. Phys. 74, (1985) 1053.
- H. J. Mang: Z. Phys. 148 (1957) 572; Phys. Rev. 119 (1960) 1069. K. Harada: Prog. Theor. Phys. 26 (1961) 667.
- I. Tonozuka and A. Arima: Nucl. Phys. A 323 (1979) 49.
- K. Varga, R. G. Lovas and R. J. Liotta: Phys. Rev. Lett. 69 (1992) 37.
- T. Fliessbach: Z. Phys. A 272 (1975) 39.
- T. Matsuse, M. Kamimura and Y. Fukushima: Prog. Theor. Phys. 53 (1975) 706.
- A. Arima and S. Yoshida: Phys. Lett. 40B (1972) 15.
- S. Yoshida: Nucl. Phys. 123 (1961) 685.
- A. Bohr and B. R. Mottelson: Mat. Fys. Medd. Dan. Vid. Selsk. 27 (1953) No. 16.
- S. Tomonaga: Prog. Theor. Phys. 13 (1955) 467, 482.
- H. Ui: Ann. Phys. (USA) 49 (1968) 69. D. J. Rowe: Rev. Mod. Phys. 40 (1968) 153; Phys. Rev. 175 (1968) 1283.
- K. Sawada: Prog. Theor. Phys. 41 (1969) 664.
- S. Takagi: Prog. Theor. Phys. 21 (1959) 174.
- T. Tamura and T. Udagawa: Nucl. Phys. 53 (1964) 33.
- S. T. Belyaev and V. G. Zelevinsky: Nucl. Phys. 39 (1962) 582.
- T. Marumori, M. Yamamura and A. Tokunaga: Prog. Theor. Phys. 31 (1964) 1009.
- T. Marumori, F. Sakata, T. Maskawa, T. Une and Y. Hashimoto: Nuclear Collective Dynamics, Lectures of 1982 Int. Summer School of Nuclear Physics (World Scientific, Singapore, 1983) 1-45.
- T. Kishimoto and T. Tamura: Nucl. Phys. A 163 (1971) 100, 192 (1972) 246, 270 (1976) 317.
- K. Takada, T. Tamura and S. Tazaki: Phys. Rev. C 31 (1985) 1948. K. Takada: ibid. 34 (1986) 750, 38 (1988) 2450.
- T. Marumori, A. Maskawa, F. Sakata and A. Kuriyama: Prog. Theor. Phys. 64 (1980) 1294.
- A. Arima: 素粒子論研究 35 (1967) E47.
- A. Arima and F. Iachello: Phys. Lett. 57B (1975) 39; Phys. Rev. Lett. 35 (1975) 1069.
- T. Otsuka, A. Arima and F. Iachello: Nucl. Phys. A 309 (1978) 1.
- N. Yoshinaga: Nucl. Phys. A 522 (1991) 99c.
- T. Otsuka, A. Arima, F. Iachello and I. Talmi: Phys. Lett. 76B (1978) 139.
- N. Yoshida, H. Sagawa, T. Otsuka and A. Arima: Phys. Lett. 215B (1988) 15.
- H. Morinaga and P. C. Gugelot: Nucl. Phys. 46 (1963) 210.
- M. Sakai: Nucl. Data Tables 15 (1975) 513, 20 (1977) 441, 31 (1984) 399.
- H. Yukawa: Proc. Phys. Math. Soc. Jpn. 17 (1935) 48.
- J. Iwadare, S. Otsuka, R. Tamagaki and W. Watari: Prog. Theor. Phys. 16 (1956) 455 and 86.
- M. Taketani, S. Machida and S. Onuma: Prog. Theor. Phys. 7 (1952) 45.
- T. Hamada and I. D. Johnston: Nucl. Phys. 34 (1962) 382. P. V. Reid: Ann. Phys. (USA) 50 (1968) 411.
- V. G. Neudatchin, Yu. F. Smirnov and R. Tamagaki: Prog. Theor. Phys. 53 (1977) 1072.
- M. Oka and K. Yazaki: Phys. Lett. 90B (1980) 41; Prog. Theor. Phys. 66 (1981) 556; Nucl. Phys. A 402 (1983) 477.
- T. Sasakawa and T. Sawada: Phys. Rev. C 19 (1979) 1498. T. Sasakawa, H. Okuno and T. Sawada: ibid. 23 (1981) 905. T. Sasakawa, H. Okuno, S. Ishikawa and T. Sawada: ibid. 26 (1982) 42.
- W. Glockle and H. Kamada: Phys. Rev. Lett. 71 (1993) 971. B. S. Pudliner, V. R. Pandharipande, J. Carlson and R. B. Wiringa: Phys. Rev. Lett. 74 (1995) 4396.
- R. Jastrow: Phys. Rev. 98 (1955) 1479.
- F. Iwamoto and M. Yamada: Prog. Theor. Phys. 17 (1957) 543.
- K. A. Brueckner: Phys. Rev. 97 (1955) 1353.
- H. A. Bethe and J. Goldstone: Proc. Roy. Soc. London A 238 (1957) 551.
- T. T. S. Kuo and G. E. Brown: Nucl. Phys. 85 (1966) 40.
- S. Nagata, H. Bando and Y. Akaishi: Prog. Theor. Phys. Suppl. No. 65 (1979).
- K. Suzuki: Prog. Theor. Phys. 68 (1982) 1627, 1999. K. Suzuki and R. Okamoto: ibid. 92 (1994) 1045.
- J. D. Walecka: Phys. Rev. 126 (1962) 653.
- K. Okamoto: Phys. Rev. 110 (1958) 143. M. Danos: Nucl. Phys. 5 (1958) 23.
- S. Fukuda and Y. Torizuka: Phys. Rev. Lett. 29 (1972) 1109. M. Nagao and Y. Torizuka: ibid. 30 (1973) 1068. T. Suzuki and D. J. Rowe: Nucl. Phys. A 289 (1977) 461.
- K. Ikeda, S. Fujii and J. I. Fujita: Phys. Lett. 2 (1962) 169, 3 (1963) 271.
- D. E. Bainum, et al.: Phys. Rev. Lett. 44 (1980) 1751. D. J. Horen, et al.: Phys. Lett. 95 (1980) 27, 99B (1981) 383. C. Gaarde, et al.: Nucl. Phys. A 369 (1981) 258.
- G. F. Bertch and I. Hamamoto: Phys. Rev. C 26 (1982) 1323.
- A. Arima, T. Cheon and K. Shimizu: Hyperfine Interact. 21 (1985) 79.
- T. Cheon, K. Shimizu and A. Arima: Phys. Lett. 38B (1984) 345.
- I. S. Towner and F. C. Khanna: Phys. Rev. Lett. 42 (1979) 51.
- T. Hoshino and A. Arima: Phys. Rev. Lett. 37 (1976) 266.
- S. Adachi and S. Yoshida: Nucl. Phys. A 306 (1978) 53.
- Y. Kawazoe, G. Takeda and H. Matsuzaki: Prog. Theor. Phys. 54 (1975) 1394.
- G. B. West: Phys. Rep. 18C (1975) 269.
- H. Bando, et al.: Prog. Theor. Phys. Suppl. No. 81 (1985).
- T. Harada and Y. Akaishi: Phys. Lett. 234B (1990) 455.
- R. S. Hayano, T. Ishikawa, M. Iwasaki, H. Ohta, E. Takada, H. Tamura, S. Sakaguchi, M. Aoki and T. Yamazaki: Nuovo Cim. 102A (1989) 437; Phys. Lett. 231B (1989) 355.
- K. Tanabe and K. Sugawara-Tanabe: Phys. Lett. 97B (1980) 337; Nucl. Phys. A 390 (1982) 385.
- I. Hamamoto and B. R. Mottelson: Phys. Lett. 167B (1986) 370, 333B (1994) 294.
- A. Arima, M. Harvey and K. Shimizu: Phys. Lett. 30B (1969) 517.
- K. T. Hecht and A. Adler: Nucl. Phys. A 137 (1969) 129.
- T. Nakatsukasa, S. Mizutori and K. Matsuyanagi: Prog. Theor. Phys. 87
(1992) 607.
* 核力は中性子と陽子を区別しない.例えば陽子-陽子間も中性子-中性子間も同じ力である.更に中性子-陽子が陽子-陽子と同じ対称性をもつ場合にはその間の力も同じである.そこでアイソスピンという概念が導入された.核子は従ってスピン自由度とアイソスピン自由度を持つ.核力はアイソスピンを保存する.更に核力が2核子間の距離のみの関数である場合,核子のスピン↑,↓,アイソスピン p, n を全く区別しない.即ちSU(4)不変である.これがスーパーマルティプレットである.このとき,SU(4)空間では4核子系まで完全に反対称状態が作られる.即ち4核子まで空間の波動関数を完全に対称にできる.N核子系の空間波動関数が完全に対称のとき[N ]というラベルを用いる.一部分が対称で一部分が反対称である場合,[N−1, 1], [N−2, 2]……というラベルをつけている.SU(4)空間の対称性と空間の対称性を掛け合せると,勿論完全反対称でなければならない.