戻る
50年をかえりみる

核反応理論の発展の一断面

河合光路

〈九州大学理学部　812-81福岡市東区箱崎6-10-1〉

1.　はじめに

今から50年前からの数年間は，それまで核反応論に君臨していた複合核模型の破綻が明らかになった時期であった．まず，Berkeleyで行われた90MeVの核子，200MeVの重陽子を用いた一連の実験で，高エネルギーの粒子が前方に強く放出されるのが観測された．複合核模型によれば，入射粒子は標的核と融合して複合核を作り，放出粒子は複合核の熱平衡状態から前後（即ち90°に対して）対称に，Maxwell型のエネルギー分布をもって，“蒸発”されるはずであった．R. Serber1) はこの現象を，入射粒子と核内核子との少数回の衝突で終る，複合核を経過しない反応，即ち直接過程によるものと解釈した．この描像で，観測された色々な反応の機構が解明された．2) 20年代に入ると，数〜10数MeV重陽子のstripping過程（3.2節参照）が発見された．3)さらに，中性子の0〜3MeVの低分解能ビームで観測された全断面積が，入射エネルギーと標的核の質量数の関数として，大きな山と谷（粗い構造）を持つことが発見され，4) Feshbach, Porter 及びWeisskopfは，それが複素一体ポテンシャル（光学ポテンシャル）による散乱として良く記述できることを見いだした．5)これが光学模型（当初は “Cloudy Crystal Ball Model" と呼ばれた）である．

私の世代が研究に参加したのはその直後である．私自身について言えば，1954年の初め（1953年度の終わり）に基研で行われた原子核理論の長期（3カ月間）研究会6)に参加したのが決定的な第一歩であった．この研究会は私にとって，また恐らく多くの若い参加者にとって，またとない“学校”であった．早川幸男教授と吉田思郎助手が“先生”であった．そこでは熱気に満ちた議論が闘わされ，友情が芽生え，共同研究が始まった．

この小文では，このシリーズの編集方針を汲んで，話を軽いイオンによる直接過程の理論に限り，この“学校”以後，私が関係した研究課題の幾つかを振り返ってみたい．ここで取り上げるのは，核の離散および連続状態への直接過程の理論で，光学模型，DWBA，チャネル結合理論，直接過程と複合核統計理論の関係等に関するものである．

2.　連続状態への遷移

基研の“学校”に行った当時，私は核内での核子の平均自由行路 (mean free path, m.f.p.) と直接反応との関係に興味を持っていた．意外にも，早川さんも同じ興味を持っておられることが分かり，すぐ菊池健君と三人の共同研究が始まった．早川さんのアイディアは，当時観測された10〜30MeVの陽子の非弾性散乱 (p, p´) で高いエネルギーの陽子が蒸発模型の予言よりはるかに強く出る，という現象を核内カスケード (Intra Nuclear Cascade, INC) 模型2, 7)で説明することだった．この模型では，入射粒子と核内核子との衝突，衝突された核子と別の核内核子との衝突の繰返しで，核内に励起した核子のカスケードが発生し，その一部が直接核外に放出され，残りは複合核を形成すると考える．

各粒子の運動，衝突を古典力学的に取り扱い，Monte Carlo の方法で事象をシミュレートする．INCは高エネルギー核反応の模型だ，と思っていた私は内心少々驚いたが，とにかくやってみることにした．Goldberger7)に従って，核に縮退Fermiガス模型を仮定し，その中での核子m.f.p.と核子-核子散乱断面積をPauli原理を考慮して計算した．低エネルギー（Fermiエネルギーの2倍以下）に対してm.f.p.をGoldberger流に計算するのは甚だ面倒であるが，幸い簡単に計算する別の方法を見つけた．入射，放出粒子の，核の平均ポテンシャルによる屈折，表面での全反射を考慮に入れた．8)計算結果は，18MeVでは過少評価であったが，31MeVではまずまずであった．

この仕事には副産物があった．その一つはm.f.p.と光学ポテンシャルの虚数部Wとの比較である．8, 9) Wがm.f.p.の逆数に比例すると仮定すると，両者のエネルギー依存性はconsistentであることが分かった．特に低いエネルギーでWが非常に小さくなるのは，二体散乱の多くがPauli原理によって禁止されることで説明される．同様な計算は同じ時期にヨーロッパでも何人かの人達によって行われ，10)同じ結論が得られた．また，核の密度の空間的変化を考慮すると，低エネルギーでWが核表面に集中することも説明された．11) Weisskopfはこの種の計算を“ふまじめ(frivolous)模型”と評したが，二体衝突に核内での有効相互作用を用いれば，それほど悪い近似ではないと思われる．但し，定量的には平均ポテンシャルの非局所性（速度依存性）を考慮しなければ，かなり過少評価になることが知られている．12)

もう一つの副産物はINCの量子力学的解釈である．INCの基本的な仮定の一つに，核内での核子-核子衝突が起こる場所が特定できる，ということがある．量子力学的には，放出波は核のあらゆる点で発生し，それらは互いに干渉するから，“衝突場所”を特定することは一見できそうにない．この問題の鍵は，観測される断面積は連続無限個の状態への遷移の断面積の平均値である，ということである．個々の状態に対応する放出波の位相が乱雑なら，問題の干渉はこの平均をとるとき相殺してしまう．実際，DWBA（3.3節）から出発し，このことを使い，入射，放出粒子の運動に対して半古典近似，核に対して局所密度Fermiガス模型を仮定すると，INCを光学ポテンシャルの影響まで取り入れて拡張した断面積の式を導くことができ，数値計算も可能である．13)現在それを使って中間エネルギーの (p, p´), (p, n) に対する実験の解析を行っている．調節パラメターなしに実験をかなりよく再現できるのが取柄である．

図1
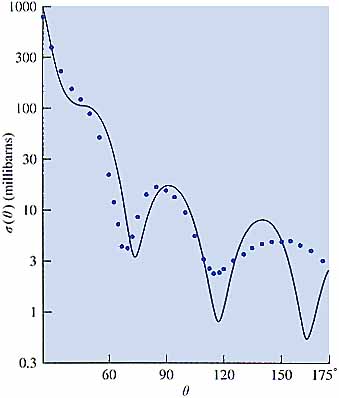
図1　初めての，縁がなだらかな光学ポテンシャルによる計算．18 MeV陽子のNiによる弾性錯乱の微分断面積の計算値（実線）と実験値（点）．(R.D.Woods and D.S Saxon: Phys. Rev. 95 (1954) 577による．)

3.　弾性散乱，離散状態への直接過程

3.1　光学模型

しかし当時，世の中の大勢は残留核の離散状態への遷移の研究に向かった．光学模型が色々な入射粒子，入射エネルギーの弾性散乱等に対して検証されていった．井戸型ではなく，なだらかな縁をもつ光学ポテンシャルによる散乱の計算がWoodsとSaxonによって初めて行われた14)（図1）．その論文に，一つの角分布の計算が電子計算機を使って15〜20分でできた，と書いてあるのを読んで，その速さに驚嘆したのを覚えている．彼らが使ったポテンシャルの形，

f(r)=[1＋exp｛(r−R)/a｝]-1

は今日Woods-Saxon型として核物理の随所に登場する．

やがて計算機が発達，普及し，光学模型による実験の解析が日常的に行われるようになった．その結果，光学模型の普遍性が明らかになり，それは全ての核反応理論の基礎になった．

3.2　離散状態への直接過程

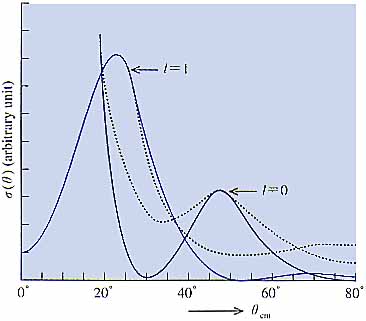
一方，直接過程による，核の束縛状態への遷移も人々の強い関心の的だった．そのきっかけは重陽子dによる，(d, p) 反応に対するstripping理論3)の成功であった．この理論によると，dの中の中性子nは標的核にはぎ取られ，決まった軌道角運動量lの殻模型軌道の一つに入る．pは反応を“傍観”するだけで，そのまま出て行く．反応が核表面付近で起こるために，pの角分布はlに強く依存する．干渉縞のような特異なものになる（図2）．これを逆に利用して，角分布から1を決めることもできる．これは反応に関与する準位のスピン・パリティの決定に非常に役立つ．実際，stripping理論の出現以後，(d, p) 反応を利用することによって，核の準位のスピン，パリティの決定が飛躍的に進んだ．

やがて，(d, p) だけでなく，核子による反応でも同様な直接反応が起こることが分かった．Austernら15)は (n, p) 反応による一粒子状態の励起を予言し，早川と笹川16)はその断面積の大きさを評価した．しかし，干渉縞様の角分布はまず17MeVの (p, p´) で観測された．17)早川と吉田18)は核子の非弾性散乱による核の集団運動の励起の機構を提唱し，低エネルギー中性子の非弾性散乱と上記の (p, p´) 反応を解析した．Brink19)も独立に同じ機構を提唱した．

これらをきっかけとして，その後色々な反応で核の離散的終状態への直接過程が発見され，それがきわめて普遍的な現象であることが分かった．その研究は核構造についての情報を得る有望な手段となり，核反応研究の中心的課題となった．

3.3　DWBA

しかし，(d, p) stripping 反応のButler理論には一つ大きな問題があった．それは断面積の角分布の特徴をよく捉えたが，細部まで正確には再現せず，大きさに対しては全く無力であった．これらの問題を解決したのが歪曲波Born近似 (Distorted Wave Born Approximation, DWBA) である．20) DWBAは (d, p) 反応だけでなく，前節で述べた (n, p) 反応の計算，16) (p, p´) の計算18,19)でも使われた．特に文献18では，以下に述べる核反応論では標準的なDWBAの定式化が与えられている．これを使った前記 (p, p´) 反応の角分布の計算が梶川ら22)によって行われ，実験とのよい一致が得られた．

DWBAは原子衝突の理論では以前から知られていた23)が，核反応論に導入されたのはこの時期が初めてである．DWBAは一次の摂動論で，反応i→fの遷移行列要素は

Tfi=〈cf(-)Ff|V−U|Fici(+)〉

で与えられる．ただし，Fi,fは始，終状態の核の波動関数である．始，終状態の粒子と核の相対運動の波動関数ci,j(±)，は普通のBorn近似と違って，平面波ではなく，歪曲（光学）ポテンシャルUi,fで歪められた波 (distorted waves) である．そのかわり，摂動は粒子と核の相互作用VからUを差し引いたものになっている．

V, U には，始，終状態いずれのものをとっても，Tfiは等しい．非弾性散乱の場合はFiとFfの直交性の故にUは寄与しない．(d, p) の場合には普通 “post form" Vf−Uf を使い，それをVnpで近似する．この近似の精度については久保24)が実例につき詳しく検討した．

反応による内部状態の遷移は形状因子

F=〈Ff|V−U|Fi〉

で記述される．但し，Fの計算に際してはV−Uに対して上記の近似をする．TfiはFのci,f(±)間の行列要素である．Fは移行角運動量lを含め，反応前後の核の準位の構造に強く依存する．表面振動の励起の場合，lはフォノンの角運動量であり，Fの大きさは振動の振幅blに比例する．(d, p) 反応ではFは f=〈Fi|Ff〉に比例する．fはFfの中でのnの一体運動の“波動関数”で，その振幅はその一体運動がFfの中に存在する確率振幅である．S=〈f|f〉を分光学的因子という．これらの量は準位の構造を知る上で非常に有益な情報である．

Sの理論的計算には始，終状態の核の構造論的知識が必要である．一核子移行反応に対しては殻模型状態，25)集団運動状態，26)対相関状態27)に対して計算が行われ，実験と比較された．(p, t) 反応の場合には，Sは移行する二つの中性子がどのような殻模型軌道に，どのような相関を持って入っているかによる．吉田は，標的核が対相関による超流動状態だと，Sが非常に大きくなることを見いだした．28)多核子移行反応のSの計算も殻模型によって行われた．29)

一方，fの空間的な動径依存性は，普通，簡単な模型で計算する．たとえば (d, p) 反応の場合，nは Woods-Saxon 型の一体ポテンシャルに分離エネルギーと等しいエネルギーで束縛されているとし，その規格化された波動関数に殻模型などで計算されたS1/2を掛けたものをfとするのである．この“分離エネルギー法”の近似は，Ffが一粒子状態に近い場合，即ちSが大きい場合には良いが，そうでなければ疑問である．もし，Fi,fが構造論で正確に与えられれば，fは定義式を使って正確に計算できる．しかし，構造論が与える波動関数は，一般に反応にとって最も重要な，核表面付近から外では当てにならない．構造論で問題になるのは核の内部だからである．

そこで，私達は一核子移行反応に対して，核の内部で正確な波動関数が分かっている時，fを無限遠まで良い近似で計算する簡単な方法を考えた．30) AusternらとSatchlerら31)も独自に類似の方法を提案した．それぞれの方法でいくつかの例に対して計算が行われた．より詳細なHartree-Fock型の計算，32) nと芯の集団運動との相互作用を入れた計算33)もなされた．分離エネルギーの方法はこれらの計算とSが大きい場合にはよく合うが，Sが小さいときには合わない．20)後になって，生井34)はN=50の同調核（中性子数の一定の核）89Sr, 90Zr, 92Mo からの (d, t) 反応のfを私達の方法で計算し，断面積の標的核の陽子数による変化を説明した．

DWBAの導入は直接反応の理論にとって画期的なことであった．それは非常に広範囲の直接反応の記述に大成功を収め，直接反応の標準的な理論の一つとなった．それは核構造について定量的な情報を引き出すことを初めて可能にし，“直接反応による核分光学”を開いた．

3.4　巨大共鳴状態の励起

これより先，Uppsalaで行われた180MeV陽子の40Caまでの核による非弾性散乱の一連の実験で，超前方（散乱角〜数度）に放出される陽子のエネルギースペクトルが測定された．35)際立った二種類のピークが観測された．その一つは励起エネルギー10数〜20MeVに対応する大きな山で測定された全ての核に対して見られた．もう一つは励起エネルギー数〜10数MeVに幾つかずつ観測された．より狭い幅のピークであった．

私達は第一の山を（実験者と同じく）双極子巨大共鳴のCoulomb励起によるものと考え，その断面積を既知の光核反応の断面積を使ってBorn近似で計算した．36)結果は理論，実験の精度を考えれば，絶対値を含めて実験とよく一致した．ずっと後になって，実はこれが当時誰も知らなかった四極子巨大共鳴の，核力による励起であることがわかったときには大いに驚いた．我々が考えた機構の断面積は，DWBAで計算するとずっと小さくなる．

第二のピークは移行軌道角運動量l=0で，スピン角運動量が移行する反応であると私達は考え，spin-flip過程と名付けた．37)これが電磁力によるものでないことは，断面積の大きさからすぐ分かった．核力による遷移の断面積の絶対値を評価するためには，なるべく理論的模型によらない評価が必要であった．計算には（平面波）インパルス近似38)を使った．核の遷移行列要素の評価には，例として良く知られた12Cの15.1MeVにある1+アイソスピンT=1の状態の励起をとり，12Nまたは12Bの基底状態から12Cの基底状態へのGamow-Teller型のベータ崩壊のft値を使って計算した．計算結果は実験の断面積を，角分布も含め〜2倍の範囲で再現した．

20Neから40Caまでの，いわゆる (s, d) 殻核に対しては，核の状態に一粒子模型やRPAを仮定し，歪曲波インパルス近似(DWIA)の計算を行った．39)これは最も初期のDWIA計算の一つである．20,40)計算結果は実験とよく合い，spin-flipという機構が立証された．この間に，藤田ら41)はGamow-Teller型の巨大共鳴が存在することを予言した．それは，約10年後，40MeVでの (p, n) 反応で初めて観測された．現在でも，中間エネルギー核反応による核のスピン・アイソスピン励起は盛んに研究されている．

3.5　DWBA計算コード

さて，このような“distorted wave の時代”の初期に困ったことがあった．それは，日本で使える大型電子計算機がなかったことである．米国に行って計算したり，実験データを米国の研究者に送って解析してもらったりする他なかった．文献39の計算も，寺沢氏が Oak Ridge で，そこで開発されたDWBAのコードを使って行ったのである．1962年〜1964年にアメリカに行っていた私は，そのDWBAコードの製作者の一人からコピーを貰う約束を得たが，結局果たされなかった．

その頃，日本にもコマーシャルな計算サービス（IBM704の使用料一時間30万円！）が行われるようになった．核研から予算を出してDWBAのコードを開発する．というプロジェクトが始まったのはこの時期である．幾人かの，主として理論のボランティアが奮闘した結果できたのが，光学模型とDWBAのINS-DWBAシリーズのコード42)である．これらはすべて核研理論部に作られたプログラム管理機関に収められ，共同利用に供された．東大計算センターができると，コードのオブジェクト・モジュールのカード・デック（！）（その製作には東大の核理論の人たちが当たった）が利用者に配られた．利用者の多くは実験家で，実験データの解析に盛んに使われた．私が関与したDWBA-2について言えば，或年の利用件数が800件を超えたのを覚えている．1ジョブで複数のデータセットが入力できたので，入力されたデータセットの数は膨大なものであったろう．

3.6　二段階過程

DWBAは大成功を収めたが，万能ではなかった．直接過程の中には，一段階では禁止または強く抑制されるものがあるからである．2フォノン状態の励起はその典型的な例である．低エネルギーでの (3He, t) 反応でも，残留核の高いスピン状態に対しては，一段階の荷電交換過程は，角運動量の不整合のために非常に強く抑制されることが分かった．外山及びSchaefferとBertsch43)は，二次のDWBAによって，この場合には (3He, a)(a, t) という二段階過程が重要であることを示した．これがきっかけとなって，(p, t)(t, d), (3He, d)(d, t), (p, d)(d, t), (p, d)(d, p´), (d, 3He)(3He, a) など色々な反応で組替え二段階過程が発見され，その多くが本会会員によってなされた．44)二次のDWBAでそれを計算するコードも作られ，45)核研のライブラリに入れられた．

3.7　チャネル結合法

時として，反応が二段階では済まず，中間状態間を無限回往復，経由する過程まで進むことがある．実は，集団運動状態の励起ではこのような場合がむしろ普通である．このような場合には摂動論展開そのものが無効である．これ対して導入されたのがチャネル結合法 (Method of Coupled Channels, CC) である．

CCでは系の波動関数Yを強く結合した状態（チャネル）1, 2,...Nの波動関数の和

YCC=c1f1＋c2f2＋...cNfN

で近似する．チャネルの内部波動関数fは既知とし，相対運動の波動関数cを未知として，Schrdinger方程式

〈fc|H−E|YCC〉=0 (c=1〜N)

から導かれるCCの基本方程式

(Ec−Kc−Ucc)cc=Sc´≠c Ucc´ cc´, (c, c´=1〜N)

を適当な境界条件のもとに解き，各cの漸近形から遷移振幅を決定する．ここに，Ecはチャネルcの相対運動エネルギー，Ucc´=〈fc|H−E|fc´〉がチャネル c, c´ 間の結合ポテンシャルである．無視したチャネルの影響は各チャネルのUccを適当な複素ポテンシャルにすることで取り入れることができると仮定する．

CCが直接過程の理論で使われたのは，吉田の (p, p´) による集団励起の計算46)が初めてである．その後，計算機の発達と相まってCCは著しい発展を遂げ，非弾性散乱による集団励起，荷電交換反応によるアイソバリック・アナログ状態の励起等の記述に大きな成功を収めた（図3）．これに対する田村，宇田川らのTexas大学グループの寄与は特に大きい．20,47)

やがて，組替え多段階過程もあることが明らかになった．この場合には始，終状態で相対運動の座標が異なるため，チャネル結合のポテンシャルUcc´は非局所型になる．私達は (d, p) 反応でdとpのチャネルが結合する場合について，定式化から数値計算まで詳しく研究した．48)一般的な組替え過程に対するチャネル結合法 (Method of Coupled Reaction (Rearrangement) Channels, CRC) は宇田川ら49)によって開発され，色々な実験の解析に応用されている．CRCは重イオン反応でも有用である50)が，ここではそれを指摘するにとどめる．

重陽子のように二つの粒子が弱く結合した粒子が関与する反応では，それがvirtualまたはrealに分解する過程が重要である．51)この過程を精度良く取り扱うには，分解状態を取り入れたCC計算をすれば良い．しかし，分解状態は連続状態であるから，そのままでは結合チャネルが連続無限個になってしまう．そこで考えられたのが離散化連続チャネル結合法 (Method of Continuum Discretized Coupled Channels, CDCC)52) である．この方法では，分解する二粒子間の相対運動量kと相対角運動量lの大きさをそれぞれ適当な上限値以下に制限する：k≦km, l≦lm. kの区間 [0, km] をN個の小区間 [ki−1, ki] (i=1〜N) に分け，各小区間を一つのチャネルと考え，適当な一つの内部波動関数で代表させる．こうして，有限個のチャネルのCC計算が可能になる．計算結果が数値的に収束するのに十分な km, lm, N を選ばねばならない．数値的収束性の入念な検討，その他の計算法の工夫，改良等の結果，CDCCはdばかりでなく，弱く結合した粒子一般の反応に対して信頼できる解析法として確立した．

この方法は現象論として成功しているが，理論的には模型空間を広げた極限での収束性の保証がない，という批判が出された．しかし最近，この問題については有望な肯定的知見が得られたと思っている．53)

このような発展の結果，今では，CCは直接過程の現象論の一般的枠組みとして確立した，と言ってよいであろう．

ここで注意すべきことは，光学模型や低次のDWBAがCCの摂動論の0ないし低次の近似ではないことである．たとえば光学模型はCCの0次ではなく，CCから弾性チャネル以外のチャネルをすべて消去した方程式の解である．チャネルcの光学ポテンシャルはUccではなく，

UcOPT=Ucc＋DUc

である．DUcは消去されたチャネルの効果を表し，dynamical polarization potential と呼ばれる．Love，寺沢，Satchler54)はそれを近似的に計算する方法を与えた．同様にDWBAもCCの一次近似ではない．この場合には始，終チャネル以外の全てのチャネルを消去するが，その答をDWBAで再現できるかどうかは問題である．非弾性散乱の場合にはそれが可能なことが示された．55)しかし，組替え反応の場合には明らかでない．

図2
図2　入射エネルギー 7.9 MeV での14N(d,p) 15N反応の角度分布のButler理論による計算値（実線）と実験値（破線）.lは移行角運動量．(S.T.Buter: Proc. Roy. Soc. 208A (1951) 559による．)
図3
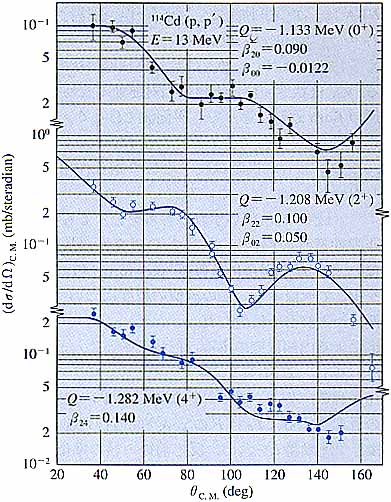図3　入射エネルギー 13 MeV での114Cd (p,p) による集団状態励起のCCによる計算値（実線）と実験値（丸）との比較．(P.H.Stelson，et al: Nucl. Phys. A 119 (1968) 14による．)

4.　直接過程と複合核過程

直接過程（以下Dと略す）と複合核過程（以下Cと略す）とは常に共存する．これらを統一的に理解することは核反応理論の基本的な課題の一つである．理論的な枠組みとして，Cに対してはS行列の分散公式，Dに対してはチャネル結合理論が存在する．早くから光学模型をS行列の分散公式から導こうとする試み56)や，低エネルギーの (d, p) 反応で，strippingと複合核過程が同時に起こる場合の理論の提唱などがなされた．57)

この問題に対する鍵はエネルギーと時間の関係である．今，エネルギーEでのS行列S(E)を，DとCによる部分SD(E)とSC(E)について

S(E)=SD(E)＋SC(E)

のように分けたとする．FriedmanとWeisskopf58)は，Dは短い時間tの幅の波束で観測されると考えた．従って，

SD(E)=〈S〉I,

ただし，〈S〉IはSのEの周りのエネルギー幅I=h/tにわたる平均値である．SC(E)はSC(E)=S(E)−SD(E)で与えられる．

佐野，吉田，寺沢59)は初めてS行列の分散公式をDとCを同時に含む形，

S(E)=SU(E)＋SV−U(E)＋Snan/(E−Wn)

に書き下した．ただし，(an)fi=gnfgni, Wn=En＋Gn/2 である．SUはDを記述するチャネル結合のポテンシャル（行列）Uによる項v，即ち SD, SV−U はハミルトニアン中の相互作用をVとするとV−Uの一次の項，第三項が共鳴項である．SU, SV−UはEと共にゆっくり変化し〈SU〉=SU=SD，〈SV−U〉=SV−Uである．共鳴項Sres=Snan/(E−Wn)はEと共には激しく変化する．しかし，そのエネルギー平均は0ではなく，〈S〉I=SD=SUから容易に分かるように，〈Sres〉I=−SV−Uである．これは共鳴項の間には相関があることを示す．SCはSC=Sres−〈Sres〉Iで与えられる．

一方，Feshbachは射影演算子による統一理論を展開した．60)波動関数のHilbert空間を入射チャネルを含む任意の部分空間（P空間）とそれ以外（Q空間）に分け，P空間を支配する有効ハミルトニアンHeffを求める．Heffの中のポテンシャルVeffのエネルギー平均U=〈Veff〉は，P空間を入射チャネルに限れば光学ポテンシャル，P空間に入射チャネルに強く結合したチャネルまで入れればチャネル結合法のポテンシャル（行列）となる．

私達はこのFeshbachの理論形式を使って，S行列を

S=SU＋Snn/(E−n)

のように，Dの部分と共鳴項，Sres=Snn/(E−n)の和の形に書けることを示した．61)ただし，(n)fi=nfni, n=En＋n/2である．〈S〉=SD=SUであるから，SCはSC=Sresで与えられる．また，〈Sres〉=0である．これは各共鳴項が互いに統計的に無相関であることを意味する．その意味でこの式は，Dが存在する場合の統計的理論を展開する場合の基礎として適している．62)

最後に統一理論の基礎としてランダム行列の理論63)があることを付け加える．ハミルトニアンの非摂動系による行列要素がランダムであると過程すると，断面積等の統計的平均が解析的に計算できることが示された．これによってDとCを統一的に取り扱う可能性が開けた．この理論による実際の計算については今後を期待したい．

5.　おわわりに

核反応の研究はその範囲と深さを着実に広げつつある．その中にあって，直接過程の理論は今なお基本的な役割を果たしている．それが築かれてきた過程で，ここに述べたような努力もあったことを知って頂けたら幸いである．言うまでもなく，ここで述べたことは核反応論研究の極一部に過ぎない．ここでは触れなかった数多くの研究と重要な寄与が本会会員によってなされたきた．それらについては別の機会にどなたかが紹介して下さることを期待したい．また，実験の論文の引用は，紙面の都合もあり，殆ど省略させて頂いたことをお断りする．最後に，初期の基研の状況などについて御教示を頂いた吉田思郎，丸森壽夫，菊池健の諸氏に感謝を申し上げる．

参考文献

  1. R. Serber: Phys. Rev. 72 (1947) 1114.
  2. 野上茂吉郎編：新編物理学選集25『高エネルギー核反応』（日本物理学会，1960）．
  3. S. T. Butler: Proc. Roy. Soc. 208A (1951) 559.
  4. H. H. Barshall: Phys. Rev. 86 (1952) 431.
  5. H. Feshbach, C. E. Porter and V. F. Wesskopf: Phys. Rev. 96 (1954) 448.
  6. 京大基研編：『京都大学基礎物理学研究所1953〜1978』(1978).
  7. M. L. Goldberger: Phys. Rev. 74 (1948) 1269.
  8. S. Hayakawa, M. Kawai and K. Kikuchi: Prog. Theor. Phys. 13 (1955) 415.
  9. K. Kikuchi and M. Kawai: Nuclear Matter and Nuclear Reactions (North-Holland, 1968).
  10. たとえば，A. M. Lane and C. F. Wandel: Phys. Rev. 98 (1955) 1524.
  11. K. Harada and N. Oda: Prog. Theor. Phys. 21 (1959) 260. K. Kikuchi: Nucl. Phys. 12 (1953) 305, 20 (1960) 601.
  12. J. Negele and K. Yazaki: Phys. Lett. 47 (1981) 71. S. Fatoni, B. L. Friman and V. R. Pandharipande: Phys. Rev. Lett. B 104 (1981) 89.
  13. M. Kawai: Prog. Theor. Phys. 27 (1962) 155. Y. L. Luo and M. Kawai: Phys. Rev. C 43 (1991) 2367. M. Kawai and H. A. Weidenm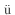ller: ibid. 45 (1992) 1856. Y. Watanabe and M. Kawai: Nucl. Phys. A 560 (1993) 43.
  14. R. D. Woods and D. S. Saxon: Phys. Rev. 95 (1954) 577.
  15. N. Austern, S. T. Butler and H. McManus: Phys. Rev. 92 (1953) 350.
  16. S. Hayakawa and T. Sasakawa: Prog. Theor. Phys. 12 (1954) 401.
  17. G. Shrank, P. C. Gugelot and I. E. Dayton: Phys. Rev. 96 (1954) 1156.
  18. S. Hayakawa and S. Yoshida: Proc. Phys. Soc. London A 68 (1955) 656; Prog. Theor. Phys. 14 (1955) 1.
  19. D. Brink: Proc. Phys. Soc. London A 68 (1955) 994.
  20. G. R. Satchler: Nuclear Direct Reactions (Oxford Univ. Press, 1983).
  21. W. Tobocman and M. Kalos: Phys. Rev. 97 (1955) 132.
  22. R. Kajikawa, T. Sasakawa and W. Watari: Prog. Theor. Phys. 16 (1956) 152.
  23. N. F. Mott and H. S. W. Massey: The Theory of Atomic Collisions, 2nd ed. (Oxford Univ. Press, 1949) p. 115.
  24. K.-I. Kubo: Prog. Theor. Phys. 44 (1990) 929.
  25. M. H. Macfarlane and J. B. French: Rev. Mod. Phys. 32 (1960) 567.
  26. S. Yoshida: Prog. Theor. Phys. 12 (1954) 141.
  27. S. Yoshida: Phys. Rev. 123 (1961) 2122; Nucl. Phys. 38 (1962) 380.
  28. S. Yoshida: Nucl. Phys. 33 (1962) 685.
  29. T. Honda, H. Horie, Y. Kudo and H. Ui: Nucl. Phys. 62 (1965) 561.
  30. M. Kawai and K. Yazaki: Prog. Theor. Phys. 37 (1967) 638. M. Igarashi, M. Kawai and K. Yazaki: ibid. 42 (1969) 245, 49 (1973) 825.
  31. A. Prakash: Phys. Rev. Lett. 20 (1968) 864. A. Prakash and N. Austern: Ann. Phys. (New York) 51 (1969) 418. R. J. Philpott, W. T. Pinkston and G. R. Satchler: Nucl. Phys. A 119 (1968) 241.
  32. K. Sugawara: Nucl. Phys. A 119 (1968) 305. K. Sugawara-Tanabe: ibid. 177 (1971) 650.
  33. I. Hamamoto: Nucl. Phys. A 126 (1969) 545, 141 (1970) 1.
  34. R. Namai: Prog. Theor. Phys. 69 (1983) 1704.
  35. H. Tyren and Th. A. Maris: Nucl. Phys. 3 (57) 35 and 52, 4 (57) 277, 637, and 662, 6 (58) and 446, 7 (58) 24 and 281.
  36. M. Kawai and T. Terasawa: Prog. Theor. Phys. 22 (1959) 513.
  37. M. Kawai, T. Terasawa and K. Izumo: Prog. Theor. Phys. 27 (1962) 404.
  38. A. K. Kerman, H. McManus and R. M. Thaler: Ann. Phys. (New York) 8 (1959) 738.
  39. M. Kawai, T. Terasawa and K. Izumo: Nucl. Phys. 59 (1964) 289.
  40. N. Austern: Direct Nuclear Reaction Theories (John Weiley & Sons, 1970).
  41. K. Ikeda, S. Fujii and J. I. Fujita: Phys. Lett. 3 (1963) 271. J. I. Fujita, S. Fujii and K. Ikeda: Phys. Rev. B 133 (1964) 549. J. I. Fujita and K. Ikeda: Nucl. Phys. 67 (1965) 145.
  42. 宇田川猛，吉田　弘，久保謙一，山浦　元：ELAST SCAT, INS-DWBA-1, INS-PT-8 (1965). 河合光路，久保謙一，山浦　元：INS-DWBA-2, INS-PT-9 (1965). （その後，岡井末二による改良が加えられた．）T. Une, T. Yamazaki, S. Yamaji and H. Yoshida: INS-DWBA-3, INS-PT-10 (1965).
  43. M. Toyama: Phys. Lett. 38B (1972) 147. R. Schaeffer and G. F. Bertsch: ibid. 159.
  44. 文献が多いので，文献20と初期のものについては下記を参照されたい．外山　学，今西文竜：素粒子論研究 52 (1976) 127. M. Kawai: in Proc. 1978 INS Int. Symp. Nuclear Direct Reactions, Fukuoka, 1978, ed. M. Tanifuji and K. Yazaki (INS, Univ. of Tokyo, 1979).
  45. TWOSTP, 外山　学，五十嵐正道，1991, TWOFNR, 五十嵐正道，1991［英訳，Y. Aoki and M. Yabe］．
  46. S. Yoshida: Proc. Phys. Soc. London A 69 (1956) 668.
  47. (a) T. Tamura: Rev. Mod. Phys. 37 (1965) 679; Annu. Rev. Nucl. Sci. 19 (1969) 99. (b) P. H. Stelson, J. L. C. Ford, Jr., R. L. Robinson, C. Y. Wong and T. Tamura: Nucl. Phys. A 119 (1968) 14.
  48. T. Ohmura, B. Imanishi, M. Ichimura and M. Kawai: Prog. Theor. Phys. 41 (1969) 391, 43 (1970) 347, 44 (1970) 1242. B. Imanishi, M. Ichimura and M. Kawai: Phys. Lett. 52B (1974) 267.
  49. T. Udagawa and H. H. Wolter and W. R. Coker: Phys. Rev. Lett. 31 (1973) 1507. W. R. Coker, T. Udagawa and H. H. Wolter: Phys. Rev. C 7 (1973) 1154; Phys. Lett. B 46 (1973) 27.
  50. B. Imanishi and W. von Oeritzen: Phys. Rep. 155 (1987) 29.
  51. R. C. Johnson and P. J. R. Soper: Phys. Rev. C 1 (1970) 976. H. Amakawa, S. Yamaji, A. Mori and K. Yazaki: Phys. Lett. B 82 (1979) 13.
  52. M. Kamimura, M. Yahiro, Y. Iseri, Y. Sakuragi and M. Kawai: Prog. Theor. Phys. Suppl. No. 89 (1986) 1. N. Austern, Y. Iseri, M. Kamimura, M. Kawai, G. Rawitscher and M. Yahiro: Phys. Rep. 154 (1987) 126.
  53. N. Austern, M. Yahiro and M. Kawai: Phys. Rev. Lett. 63 (1989) 2649. N. Austern, M. Kawai and M. Yahiro: Phys. Rev. C 53 (1996) 314.
  54. W. G. Love, T. Terasawa and G. R. Satchler: Nucl. Phys. A 291 (1977) 183.
  55. S. K. Penny and G. R. Satchler: Phys. Lett. 5 (1963) 212.
  56. G. E. Brown: Rev. Mod. Phys. 31 (1959) 893.
  57. R. G. Thomas: Phys. Rev. 100 (1955) 25. M. Nagasaki: Prog. Theor. Phys. 16 (1956) 429. H. Ui: ibid. 299.
  58. F. L. Friedman and V. F. Weisskopf: in Niels Bohr and the Development of Physics, ed. W. Pauli (Pergamon, London, 1955).
  59. M. Sano, S. Yoshida and T. Terasawa: Nucl. Phys. 6 (1958) 20. M. Sano: Prog. Theor. Phys. 27 (1960) 180.
  60. H. Feshbach: Ann. Phys. (New York) 5 (1958) 357, 19 (1962) 287; Annu. Rev. Nucl. Sci. 8 (1958) 49.
  61. M. Kawai, A. K. Kerman and K. W. McVoy: Ann. Phys. (New York) 75 (1973) 156.
  62. H. Feshbach: Theoretical Nuclear Physics, Nuclear Reactions (John Wiley & Sons, 1992).
  63. H. Nishioka, J. J. M. Verbaarschot, H. A. Weidenmuller and S. Yoshida: Ann. Phys. 172 (1986) 67. H. Nishioka, H. A. Weidenmuller and S. Yoshida: ibid. 183 (1988) 166.