戻る
50周年特別寄稿

非線形波動の物理と応用--光ソリトンによる超高速光通信--

長谷川　晃

〈大阪大学工学部電子情報通信工学専攻　565大阪府吹田市山田丘2-1〉

1.　はじめに

1996年春，米国の光学会において1チャンネル当たり毎秒10ギガビット，8チャンネルの合計で毎秒80ギガビットの光ソリトン信号を，1万km以上にわたり無エラーで伝送することに成功したとの報告がなされた．非線形波動の応用を考えた場合，理論的にもまた実用的にも恐らく最も成功した例が，ここで紹介するファイバー中の光ソリトンであろう．

筆者がTappertと共にファイバー中に光ソリトンが存在することを理論的に示して1)から，今年で23年目になる．この間に光ソリトンの研究は多くの紆余曲折を重ねながらめざましい発展を遂げ，21世紀に向けての超高速光通信信号の担い手として大きな期待がかけられている．1965年にソリトンという語が誕生2)してから約30年，日本物理学会の50周年のほぼ6割の時がたつ．中でも光ソリトンは，先端技術への応用とその中でソリトン理論が非常に有効に使われてきたという歴史を持ち，特に興味ある進展を遂げてきた．本論文では非線形波動の中，主に光ソリトンの物理と応用に焦点を当て，その歴史を振り返ってみたいと思う．

光ソリトン研究の歴史を振り返ると，まず第一段階として光ソリトンの存在の理論的証明から実験的検証までのほぼ10年間，つづいて光増幅器のみを用いた（中継器を用いない）全光学的長距離光伝送システムの考えの誕生と，その実験的検証の段階，続いてこうした超長距離光ソリトン伝送系で発生する諸問題の認識とその解決法の導出，そして最近の光ソリトンを用いた波長分割多重システムの理論と実験的検証の各段階に分けて考えることができる．筆者はこれらの歴史の各段階に密接に関わり，その進展を眺めてきた．この論文ではこうした歴史的発展に沿って，やや個人的な立場ではあるが光ソリトンの研究を紹介したい．

2.　ファイバー中の光波の包絡線

誘電体ファイバーは，その性質から分散性と非線形性を持つ．非線形性は誘電体分子の作るポテンシャルが対象の場合，分極率の三次の非線形性（Kerr効果）に帰因する．また分散性は誘電率の波長依存性と導波特性から発生する．（群速度）分散性のため局在した光波（光パルス）は変形を受ける．通常の分散シフトファイバーの場合，パルス幅10ピコ秒程度の光波の包絡線を考えた場合，光波の強度が数ミリワットの場合，非線形性が生む自己位相変調による周波数の変化の大きさと群速度分散によるパルス幅の広がりは，ほぼバランスする．複素包絡線関数を(T,Z)とした場合，長谷川とTappert1)はが非線形Schrdinger方程式

を満たすことを導き，1973年にファイバー中の光波の包絡線がソリトンを作ることを理論的に示した．式(1)でZはファイバーの分散距離 （群速度分散によってパルス幅が2倍になる距離）で正規化した軸方向の距離，Tはパルス幅で正規化し群速度で動く座標に乗った時間をあらわし，はKerr係数で正規化した包絡線の複素振幅，さらにGは分散距離あたりのファイバー損失をあらわす．

厳密にはファイバー中の電磁波はファイバーの断面で強度が変化する三次元の場であるが，その軸方向の変化の割合がファイバー断面の変化に比べてはるかに緩やかである仮定のもとに，三次元の波動方程式を式(1)のような形に逓減することができる．3)また一般にファイバーの持つ高次の分散性や，非線形性（Raman効果）なども付け加えることができる．こうした場合，非線形係数はファイバーの断面で平均化した強度を用い，また分散特性は各モードの導波特性と誘電体固有の分散特性の両者を考慮したものを用いるとよいことが証明される．ここで大事なことは，式(1)が成り立つためには，いわゆる単一モードファイバーを想定する必要があることで，多くのモードが同時に存在する場合には各モードの包絡線に対して結合した連立非線形Schrdinger方程式を解く必要がある．通常単一モードファイバーにおいても光波の偏波方向により二つの偏波が存在するため，厳密にはそれぞれの偏波に対する結合非線形Schrdinger方程式を考えなければならない．しかし幸い偏波面は普通極めて短い距離（数メートル以下のオーダー）で頻繁に変化するため，各偏波に対する結合非線形Schrdinger方程式を少し長い距離にわたって平均化すると，各偏波モードの振幅の和として新たに定義された光波包絡線は式(1)を満たすことも証明されている．4)式(1)でファイバー損失を無視した場合の理想的非線形Schrdinger方程式に対する逆散乱法はZakharovとShabat5)によって導かれた．Laxの固有値方程式6)はこの場合G＝0とした式(1)の解をポテンシャルとして

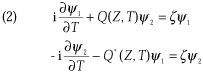
とかくことができる．逆散乱法の理論から式(2)の固有値xはが非線形Schrdinger方程式（式(1)でG＝0とした式）を満たす限り一定（Zに無関係）であり，またソリトンはxの離散的固有値であらわすことができる．式(2)は一般に離散的固有値と連続固有値の両方を持つ．この結果ファイバーに適当な光パルスを入力すると，パルスは式(2)の離散的固有値の数に相当するソリトンと連続固有値が示す線形分散波の集合としてファイバー中を伝送する．作られるソリトンは式(2)の固有値の実部を速度（および周波数）とし，虚部を振幅（およびパルス幅の逆数）とするため，KdVソリトンの場合と異なり，発生したソリトンの速度は振幅に無関係に決まる．これはソリトンを用いる光通信において非常に重要なことであり，ソリトンが通信に有効に使われるための必要条件となる．

筆者がファイバー中の光ソリトンを発見した当時のいきさつを少し振り返って記述しておこう．当時，非線形Schrdinger方程式が孤立解を持つことは光の自己収束やプラズマ中の波動の包絡線の伝搬で知られていた．まだソリトンに対する考えが生まれて間もないころであったが，当時名古屋大学プラズマ研究所の教授をしておられた谷内俊弥先生がいち早くソリトン現象に興味を持ち逓減摂動論などを展開しておられ，私なども先生に弟子入りをしてソリトンの勉強をさせてもらっていた．1968年にBell研究所に移ってからもプラズマ中の電磁波の非線形現象，特に磁気圏を伝搬するホイッスラー波の作る変調不安定性や包絡線ソリトンに関する研究を行っていた．この時，高い周波数の波（ホイッスラー波）の包絡線と低い周波数の波（Alfvn波）が結合することによりソリトンが発生することも発見したが，7)これは後にZahalov方程式と呼ばれる方程式として知られるようになっている．

3.　全光学的長距離光ソリトン伝送システム

ファイバー中に光ソリトンが存在することは後（1980年）にMollenauerらが実験的に検証することに成功した．8)この時のMollenauerの興奮した電話の声が今も筆者の耳に残っている．実験的検証に7年もの年月を要した理由は，低損失のファイバーが当時存在しなかったことと，ソリトンをつくるための波長可変型高出力光源が存在しなかったことにある．このためMollenauerらは色素レーザーを製作し，これを実験に使った．ちなみに現在，光源として使用されている半導体レーザーは1980年の中頃に発明されたものである．Mollenauerらの実験に気を良くした児玉（当時Bell研究所のポストドックをしていた）と筆者は，ソリトンが分散性による波形歪みを起こさないことからファイバー損失を補うために光増幅器のみを用い，中継器を用いない全光学的長距離通信システムを提唱した．9)当時光通信では分散性による波形歪みの整形を行うための中継器が必要とされ，これが通信速度の高速化（高密度化）のネックとなっていた．

当時まだ光増幅器が開発されていなかったため，筆者はファイバー中のRaman効果を用いるとファイバーそのものを光増幅器とすることができると考え，これによるソリトンの長距離伝送を理論とシミュレーションで証明した．10)Mollenauerらは再びこのアイデアを取り上げ，パルス幅40ピコ秒のソリトンの初めての長距離(6,000 km)伝送に成功した．11)1989年，日本での国際学会でMollenauerがこの話をした時，「長谷川がファイバー中にソリトンが存在することを唱えた時にクレイジーだと思ったが，Raman増幅でソリトンが無歪みに長距離にわたって伝送する話を聞いた時にはもっとクレイジーと思った．しかし実験をしてみると上手くいった．」という前置きで講演したのを今も覚えている．つまりファイバー中の光ソリトンや，その長距離伝送に関する考えは，光ソリトン実験の先駆者であるMollenauer自身でさえ当時半信半疑であったのだ．したがって他の光通信関係の研究者が長い間ソリトンに目を向けなかったのも無理ないことである．

1987年にエルビウムをドープしたファイバー(EDFA)が，丁度ファイバー損失が極小となる波長1.55ミクロンの光波を効率よく増幅することを発見された12, 13)NTTの中沢氏らは，ただちにEDFAを用いた長距離光ソリトン伝送の実験に成功し，14)その後，各国で興味あるソリトン伝送実験結果がいくつも報告されるようになった．

ファイバーに沿って周期的に増幅器を置いた場合，包絡線の振舞を記述する式は，式(1)の右辺に周期的な（Zの関数とした）増幅効果を表す項をつけ加えることによって記述できる．しかし実際の実験データから得られる正規化された減衰率Gおよび増幅器の利得を評価するとO(1)以上の大きさとなることが分かり，我々はこのような大きな摂動項の加わった非線形Schrdinger方程式がソリトン解を持つかどうかに興味をもった．その結果，1991年に児玉と筆者は，最低次では増幅器間隔ZaでZ方向に激しく振動する包絡線振幅が存在し，その包絡線部分を取り除いた振幅が満たす方程式が，Lie変換の手続きをすることにより非常に良い近似で摂動項を伴わない非線形Schrdinger方程式に逓減できることを証明することができた．15)我々はこの手法が磁場中の荷電粒子のガイディングセンター理論と類似していることから，こうして得られたソリトンをガイディングセンターソリトンと名付けた．磁場中の荷電粒子はLarmor運動をしながら，そのLarmor半径の中心はスムーズな動きをする．光ソリトンの場合も減衰と増幅を繰り返しながら激しく振動する光波の振幅のガイディングセンターはスムーズな動きをし，ソリトン解を持つのだ．しかし磁場中の粒子のガイディングセンターの場合と違い，ソリトンの場合は方程式そのものの変換，すなわち無限次元のLie変換を行う必要があり，これには児玉が既に発展させていた理論16)が大きく役立った．磁場中の粒子のガイディングセンターの動きは正準変換で断熱不変量を導入することでも求められるが，Larmor半径の全てのオーダーまで有効な変換をするにはLie変換が適していることも付記しておく．

4.　長距離光ソリトン伝送における問題点の認識

日米間の光通信を考える場合，ほぼ9,000 kmにわたって無エラー（ビット誤り率が10−9以下）の伝送を確保しなければならない．1.55ミクロンという光の波長で眺めた場合，この距離は1013程度のオーダーとなる．ソリトンは強靱な波形をもっているが，このような大きな距離にわたって伝送を続けると各種の擾乱によってわずかながら波形歪みが生じ，またソリトンの時間位置や振幅などの，いわゆるソリトンパラメーターが変化する．1987年GordonとHaus17)は増幅器の雑音がソリトンの速度に変調を与え，時間ジッターの原因をつくるという理論を出し，10ギガビット程度のソリトン信号は5,000キロ以上無エラーで伝送させることはできないと主張した．他方ではまたソリトン間隔を詰めて伝送すると，二つのソリトン間の相互作用が同じような時間ジッターを発生させるため，これが原因となってソリトンの高密度長距離伝送が困難になるという理論も出現した．さらにソリトンを用いて波長分割多重通信を行う場合，理想的な線路であれば各波長チャンネルのソリトンは逆散乱理論の結果その性質を失わずにすれ違うだけであるが，たまたま光増幅器を通過中に衝突すると(2)式の固有値の変化が発生し，これが同様にソリトンパラメーターに擾乱を与え，伝送障害の原因となることも分かった．特にGordon-Haus効果と呼ばれる光増幅器の雑音の影響は雑音が原因しているだけに，ソリトンの最大伝送距離を決定的にするものと思われていた．

当時筆者はBell研究所にいて太平洋横断9,000 kmの海底光ケーブル用の伝送方法について専門家達と種々検討をしていたが，従来の線形方式による伝送結果に比べ，ソリトンの方はGordon-Haus効果のため伝送距離が延びず苦労した月日が続いた．1991年の春，児玉と筆者はこの問題を解決するために搬送波周波数を中心とする狭帯域のフィルターを用いることを提案した．18)このフィルターを用いると，ソリトンの振幅と周波数（Lax方程式の固有値）はその位相空間である値に収斂することが示され，この方法によりGordon-Haus効果が制御されることが証明できた．この提案をもとにMollenauerらは1週間でソリトンの伝送距離を2倍にすることに成功し，ソリトンの長距離伝送に対して指針を与えることになった．この方法は雑音と信号を分離するという，従来線形信号では不可能と考えられてきたことを可能にするという意味で，ソリトンを用いた通信の一つの大きな特徴となる．このようなことが可能であるのは，固有値方程式(2)の離散的固有値によって表されるソリトンと連続固有値で表される線形波や雑音が本質的に直交しているからであり，この結果ソリトンパラメーターをその位相空間で自由に動かすような制御を行うことにより，信号と雑音を分離することが可能になるのだ．フィルターを用いてソリトンを制御する方法は同時にMeccoziらによっても発見された．19)しかし，これらの方法は後にフィルターの中心周波数辺りの線形波を異常に増大させ，それがひいてはソリトンを破壊させることが知られ，それに対する解決法が要求されるに至った．Mollenauer達はフィルターの中心周波数を伝送方向に徐々に変化させることにより，この問題を解決した．20)一方，ソリトンを伝送途中に制御することにより伝送距離を引き延ばすアイデアは，その後多くの研究者から発表され，中でも中沢らはソリトンの増幅器の利得をソリトン列に同期させて時間的に変調を加えることにより，実質的に無限の距離にわたってのソリトン伝送に成功した．21)ソリトン制御の結果1990年代の前半はソリトンの方が，伝送速度の上でも伝送距離の上でも，線形波をはるかに上回る結果となった．

5.　波長分割多重通信

しかし1995年になって線形波伝送を研究するグループは群速度分散が零となるファイバーを開発し，20波の波長分割多重の方法で毎秒100ギガビットの超高速通信の8,000 km程度の距離に渡る伝送実験に成功した．ここでいう線形波は，いわゆる Not Return to Zero (NRZ) パルスを用いたものである．これは1がいくつも続いた場合のデジタル信号をパルス幅の大きさで表した矩形波を用いた伝送方法である．1チャンネル当りで伝送速度をあげようとすると，SN比を充分とるために信号電力を大きくする必要があり，結果として非線形効果が発生し，たとえ群速度分散が0になるようなファイバーを用いても波形歪みを伴うことが分かっている．この結果，1チャンネル当りの伝送速度はNRZ方式では毎秒5ギガビット以上にすることは困難とみなされている．そこで波長分割多重を用い，さらにこの障害を乗り越えるため初期の波形に位相変調を加え非線形歪みを補正することに成功したのだ．これに対しソリトン通信では1チャンネル当りの伝送量ではNRZ方式をはるかに上回るが，波長分割多重をおこなうと前述の増幅器内でのソリトン同志の衝突に起因する時間ジッターが災いし，トータルの通信量としてNRZほど大きくならない問題を抱えていた．1995年夏，筆者らはこの問題を解決するために，ファイバーの分散値を増幅器直後で大きくし，増幅器直後で非線形効果の増大に見合う分散値の増大を確保することにより，周期的に増幅器が存在するファイバー線路においてもソリトンに理想的な線路と同じような振舞をさせることを考えた．このためにはファイバーの分散値を増幅器の位置でステップ状に大きくし，その後ファイバー損失に合わせ指数関数的に減少させると理想的な線路を作ることができる．しかしこのようなファイバーの製作は困難であるため，階段状に分散値を増加減少させることを考え，この場合について衝突による時間ジッターの大きさを評価し，階段の数Mを充分大きくとると，衝突による時間ジッターがMの4乗に逆比例して減少することも示した．22)この方法を知ったMollenauerたちは直ちにこれを実験に採用し，周回実験を用いて1チャンネル当り10ギガビットのソリトンを用い8チャンネルの波長分割多重を行い，合計80ギガビットのソリトン信号を1万キロ以上にわたり無エラー伝送することに成功した．23)

ソリトン伝送を線形波伝送と比較した場合，次の2点で本質的な違いが存在する．一つはソリトンの振幅は式(2)の有限個の離散的固有値（ソリトンパラメーター）の振舞で記述できるのに対し，線形波の記述には連続固有値のもつ無限個の自由度を必要とする点である．このことはソリトンは本質的にデジタル通信に適しており，またソリトン系でのシステム設計やソリトン制御は有限個の自由度のみを基本にしてできることを意味している．第二は線形波では伝送経路が生み出す各種の波形歪みの原因を入力側で調整しなければならないのに対し，ソリトンは擾乱が存在しても波形は歪まずソリトンパラメーターのみが摂動を受ける性質を持つため，この自己保存の性質を用いて伝送線路の途中で制御を行うことができることである．この違いは射程を全て初期条件で決定する無誘導ロケットと，これを途中で制御する誘導ロケットの相異に類似している．この場合，線形波の調整には無限個のパラメーターの調整を必要とするのに対し，ソリトン制御には有限個のソリトンパラメーターの制御のみですむことは言うまでもない．

6.　結　言

光ソリトンを高速通信に用いるという考えは，ファイバー中の光波の包絡線がソリトンを作るという考えから出発した．続いてこれはファイバーの損失を光増幅器を用いて周期的に補償することによる超長距離伝送の考えに発展した．この間ソリトン理論を用いることにより多くの障害を乗り越え，現在では波長分割多重を用い毎秒80ギガビットという大量の情報を1万キロ以上にわたり無エラー伝送することに成功するに至った．今後も伝送速度はさらに大きくなることが予想される．この歴史を振り返って特に印象深い点は，逆散乱法を中心とするソリトン理論という今世紀の応用数学の重要な成果が超高速光通信という先端技術に的確に応用されたことである．20世紀の一大発見であるソリトンとそれに関係する応用数学の成果がこのような形で先端技術に見事に適用されてきたことは，筆者自身も驚きを感じている．筆者の強力な共同研究者である児玉裕治が学位論文でソリトンの摂動論をやっていた頃，筆者は冗談にソリトン理論そのものが摂動論にもとづいているのにもかかわらず，さらにその摂動論をやるということは数学的には興味があるかもしれないが，全く実用的価値がないのではないかとよく冷やかしていたものである．驚くべきことに超高速ソリトン伝送においては児玉の開拓したソリトンの摂動論が威力を発揮し，その結果が実験結果と非常に良く一致するという形であらわれている．ファイバー中の光ソリトンは単に先端技術の応用としてのみならず，ソリトン理論の優秀さを実験的に確証した点でも大きな貢献をしたと言えよう．

参考文献

  1. A. Hasegawa and F. D. Tappert: Appl. Phys. Lett. 23 (1973) 142.
  2. N. J. Zabusky and M. D. Kruskal: Phys. Rev. Lett. 15 (1965) 240.
  3. Y. Kodama and A. Hasegawa: IEEE J. Quantum Electron. QE-23 (1987) 1938.
  4. C. R. Menyuk: IEEE J. Quantum Electron. QE-23 (1987) 174.
  5. V. E. Zakharov and A. B. Shabat: Sov. Phys.-JETP 34 (1972) 62.
  6. P. D. Lax: Commun. Pure Appl. Math. 21 (1968) 467.
  7. A. Hasegawa: Phys. Rev. A 1 (1970) 1746.
  8. L. F. Mollenauer, R. H. Stolen and J. P. Gordon: Phys. Rev. Lett. 45 (1980) 1095.
  9. Y. Kodama and A. Hasegawa: Opt. Lett. 7 (1982) 339.
  10. A. Hasegawa: Opt. Lett. 8 (1983) 650.
  11. L. F. Mollenauer and K. Smith: Opt. Lett. 13 (1988) 675.
  12. R. J. Mears, L. Reekie, L. M. Jauncey and D. N. Payne: Electron. Lett. 23 (1987) 1026.
  13. E. Desurvire, J. R. Simpson and P. C. Beeker: Opt. Lett. 12 (1987) 888.
  14. M. Nakazawa, Y. Kimura and K. Suzuki: Electron. Lett. 25 (1989) 199.
  15. A. Hasegawa and Y. Kodama: Phys. Rev. Lett. 66 (1991) 161.
  16. Y. Kodama: J. Stat. Phys. 39 (1985) 597.
  17. J. P. Gordon and H. A. Haus: Opt. Lett. 11 (1986) 665.
  18. Y. Kodama and A. Hasegawa: Opt. Lett. 17 (1992) 31.
  19. A. Mecozzi, J. D. Moores, H. A. Haus and Y. Lai: Opt. Lett. 16 (1991) 1841.
  20. L. F. Mollenauer, J. P. Gordon and S. G. Evangelides: Opt. Lett. 17 (1992) 1575.
  21. M. Nakazawa, K. Suzuki, E. Yamada, H. Kubota and Y. Kimura: Electron. Lett. 29 (1993) 729.
  22. A. Hasegawa, S. Kumar and Y. Kodama: Opt. Lett. 21 (1996) 39.
  23. L. F. Mollenauer, P. V. Mamyshev and M. J. Neubelt: Electron. Lett. 32 (1996) 471.