このページでは、物理学会誌「新著紹介」の欄より、一部を、紹介者のご了解の上で転載しています。ただし、転載にあたって多少の変更が加わっている場合もあります。また、価格等は掲載時のもので、変動があり得ます。

量子力学の数学理論；摂動論と原子等のハミルトニアン

加藤敏夫稿，黒田成俊編注

近代科学社，東京，2017，xx＋434p，24×19 cm，本体8,000円［専門向］ISBN 978-4-7649-0545-0 C3042

紹介者：江沢　洋(学習院大理)

本書は量子力学の数学を一歩一歩ていねいに描いた，ありがたい本である．同じ方面の本にvon Neumannの『量子力学の数学的基礎』があるが，こちらは数学的基礎をうちたてるための枠組みを提示したもので，その枠組みに盛り込むべき内容を描き出してはいない．物理量を表す演算子は自己共役でなければならないとしたが，水素原子のハミルトニアンですらそれを証明していない．本書の主題は，その証明をし，証明の基盤となる摂動論の基礎づけをすることである．
著者の加藤は東大物理の助教授として吉田耕作，小平邦彦らと関数解析の黄金時代を築いたが，1962年にカリフォルニア大学バークレイ校に転じ，1999年に没した．遺著にPerturbation Theory for Linear Operators, Springer（1966, 1976）の大作などがある．遺された大量の研究資料の中から本書のもとになった原稿は発見された．その緒言に記された日付から1945年6月に一応の完成をみたものと分かる．それをお弟子のひとり黒田成俊が整理し懇切な補注をつけて本書はできた．
本書を開くと，「演算子はその定義域を与えなければきまらないことは自明のことであるが，一般の物理学者にとっては注意すべき事柄である」に出会う．その後にも「エルミート演算子もその定義域が与えられなければ意味がない．量子力学においてはこれが明確に定義されないことが多いから特に注意が必要」と繰り返す．この書評では，このことを強調する本書の雰囲気が多少なりとも伝えられたらと思う．
ほとんどの物理の教科書は演算子のエルミート性と自己共役性は同義としているが，数学では違う．前者は「演算子Rの定義域D(R)の中に収束列｛f_k｝があれば極限f_k→fをD(R)に加え，その結果である［D(R)］が考えているヒルベルト空間に一致する場合に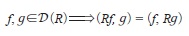

となるなら（āをaの複素共役として （af, g）＝a（f, g）, （f, ag）＝ā(f, g)としている点，物理の慣行と違う）Rをエルミート演算子という」と定義されているが，後者に対してはエルミート演算子Hであることに加えて「∀f∈D(H)　⇒（Hf, g）＝（f, g*）となるg, g*に対してg∈D(H)かつg*＝Hgとなること」が要求されている．自己共役であって初めて射影演算子E(λ)を用いたHの対角化 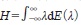が可能になり，観測との関係が成り立つのだから自己共役性は重要である．
さて，問題は原子のシュレーディンガー演算子H_S＝T＋V，ただし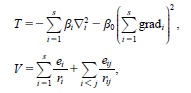

（の拡張）を自己共役演算子として定義することである．
実は，運動エネルギーの演算子を，フーリエ変換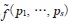の世界で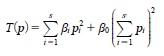

をかける演算子として，定義域を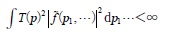

という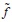の全体とするアプローチがあり，VがTに関しminorな演算子であることから同じ定義域DでT＋Vが自己共役になることを示す．VがTのminorな演算子だとは，定義域の広さを⊃で表せばD(V)⊃D(T)であること．しかし，これではTが微分演算子であることが見え難くなるというのか，加藤は別の方法も提示している．
まず，定義域を「条件（i）任意のx_kにつき何回でも微分でき，（ii）どんな多項式P（x₁, ..., x_s）をかけても遠方 |x₁|＋...＋|x_s|→∞で0に収束する」をみたす関数f（x₁, ..., x_s）の全体D*に限ったH_Sを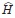と書く．H_Sの微分演算子はD*より広い範囲で意味をもつのでH_S⊃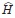である．
一般に，演算子Rの定義域がD(R)のとき与えられたf∈D(R)に対し，その部分集合D₁でf_n→fとなる列｛f_n｝をもつものがあればそれをRの準定義域という．またf_n∈D(R)，f_n→f，Rf_n→f*ならf∈D(R)，f*＝RfとなるときRを閉演算子という．Rが線形閉拡大をもてば，その中の最小のものを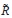と書く．
われわれの問題に戻ってH_S, 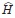の線形閉拡大は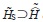となる．また，VはTのminorな演算子だからD^*はHの準定義域となり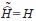となる．よって 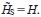ところがHは自己共役だったから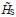も自己共役である．こうして微分演算子を含むH_Sからの拡大として自己共役な演算子が得られた．
本書では，さらに進んでH₀に加える摂動αVからminorの条件をはずすと固有値のαに関する展開も許されなくなることを解けるモデルで示し，regularな摂動の概念を導入して3次までの漸近展開を調べ誤差の評価を与えている．次に量子力学的な状態の変化に対する摂動論に移り，初期状態ψ₀がVの定義域に入っていても摂動Vの高次の項は定義域を飛び出す恐れからVがかけられなくなり有限次で止まるほかないと指摘している．その結果から遷移確率を計算してエネルギーの保存をいい，あるいはWigner-Weisskopf流の摂動計算で遷移確率をe^－Γ_tに比例するとする論法を鋭く批判しており，未開の地であることを感じさせる．
巻末に補遺と付録「加藤敏夫先生とE. C. Kemble氏の書簡交換について」（岡本久），「Schrödinger方程式の数学―その生誕と成長」（中村周）を添える．
本書は一歩一歩綿密に論を進めてゆくので読み進めるには忍耐を要するが，読み終えたら確実さが手に入る．物理からも挑戦する人の現れんことを！
（2018年6月18日原稿受付）

ページの頭に戻る

Non-Hermitian Quantum Mechanics

Nimrod Moiseyev

Cambridge Univ. Press, UK, 2011, ix＋394p, 26×18 cm, $160.00［専門～学部向］ISBN 978-0-521-88972-8

紹介者：明　孝之(大阪工大工)

本書では量子力学における共鳴状態を，複素エネルギー固有値を持つ崩壊状態として考えることを発端として，非エルミート系の量子力学の理論体系，及び実際の物理系への適用を紹介している．共鳴状態は物理学の幅広い分野で観測される現象であり，量子力学における共鳴状態の記述には様々な方法が存在する．その一つとして，複素固有値を許す非エルミート系の量子力学を導入することで，共鳴状態をS行列の極として定義することができる．本書では極として記述される共鳴状態を含めた非束縛状態を扱う理論と，その実用的な計算法を紹介している．
本書の構成は，1章で概観を述べた後，いきなり非エルミート系を導入するのではなく，まずは2章にて典型的な形状共鳴やフェッシュバッハ共鳴を説明している．3章ではエルミート系の量子力学に基づく実エネルギー状態としての共鳴状態の記述，および共鳴状態と散乱問題との関係を説明している．共鳴状態を扱う計算法も紹介されている．4章以降から本筋である非エルミート系量子力学の説明に入る．非エルミート系量子力学では，共鳴状態の波動関数の境界条件を外向き波として定義するが，その結果，波動関数の漸近形が発散することになり理論的な困難が生じる．例えばノルムの定義はどうするのか？　共鳴状態の物理量は複素数になるが，それはどのように解釈されるのか？などの素朴な疑問が挙げられる．5章では，これらの問題の解決法となるハミルトニアンの相似変換を幾つか紹介している．特に「complex scaling method（複素スケーリング法）」とよばれる方法が中心となっている．この方法は粒子座標を複素平面に拡張する変換である．この変換により共鳴状態の境界条件が束縛状態と同じものになり，大変扱いやすくなると同時に多体問題にも拡張できる．本書の多くの説明でもこの変換が活用されている．ちなみに表紙のサイコロには複素スケーリングで変換されたシュレディンガー方程式が描かれている．
非エルミート系では内積や完全系の定義，エネルギー変分原理もエルミート系とは異なる．6章，7章において，それらの丁寧な説明，及び共鳴状態を求めるための基底関数展開などの実践的な例題を豊富に載せている．実際の計算で注意すべき箇所の指摘もなされている．8章では散乱理論への適用があり，散乱物理量の計算に有用なグリーン関数を導入している．このグリーン関数を使って共鳴状態の効果を分析する説明があるが，詳細には触れられていない．この章では時間依存の散乱問題も紹介されている．
本書の特徴として，随所にエルミート系との違いを述べた上で非エルミート系での説明がされているので理解がしやすい．より高度な内容に触れたい読者用にも各章に文献がふんだんに載っている．更には多くの演習問題が載っており，通常の量子力学演習を非エルミート系に発展させたような内容になっている．その解答も実に丁寧に記されており大変有り難い．
現役の研究者が理論体系を学び，実践的な技術を習得するためにはうってつけの本であると共に，学部生・大学院生にとっても非エルミート系，共鳴状態の物理を基本から学べる良書となっている．
（2018年8月10日原稿受付）

初歩から学ぶ固体物理学

矢口裕之

講談社，東京，2017，vi＋312p，26×19 cm，本体3,600円［学部向］ISBN 978-4-06-153294-6

紹介者：望月維人(早大先進理工)

研究室に配属された学部4年生に，卒業研究の本格的な研究テーマを与える前に，教員は彼らに基礎的な知識をしっかりと叩き込む必要がある．しかし，そのための最適な教科書を探すのは，どの分野の先生方も意外と苦労されているのではなかろうか？　私の物性理論の研究室でも，1年の前半を教科書の輪講に当てており，卒研生には例年一，二冊の教科書を読ませている．名著と呼ばれる教科書は数多いが，本書は物性物理や固体物理を学ぼうとする卒研生のための最適な書のひとつである．
本書は，一見「固体物理学の普通の教科書」に見える．しかし，学部4年生の視点と頭脳レベルになって，彼らが何につまずくのかを想像しながら読んでみると，良くできた教科書であることが実感できる．本書は次のような特徴を備えている．
理由1：量子力学と統計力学の基礎にページを割いている
通常の固体物理の教科書は，読者が量子力学や統計力学を習得済みという前提で話を進めている．もちろん本来はそうあるべきなのだが，そこはまだこれらの科目を習いたての学部4年生である．知識はうろ覚えだ．本書では，固体物理学につながる量子力学と統計力学の知識をしっかりとおさらいすることで，基礎科目から，それらに立脚した一段上の「固体物理学」につまずくことなく学習を進められるように編まれている．
理由2：掘り下げ方が適度
「固体物理学」の名著と呼ばれる教科書は数多いが，多くの教科書では，各章でそれぞれのテーマが深く掘り下げられている．初学者にはそれが重すぎて，最初の数章を何とか読み切ったあとに，疲れて挫折してしまうことはないだろうか？　本書は，各テーマの基礎的で面白い部分にしっかりフォーカスした内容になっており，そのおかげで，卒研生でも固体物理学を俯瞰的に学習し，その中から興味を持ったことを（他の教科書で）さらに自分で掘り下げることができるような構成になっている．
理由3：計算の途中式が丁寧　
学部時代の授業や演習では，計算の途中式や論理の流れが逐一丁寧に説明される．それに慣れている卒研生が，はじめて教科書を輪講する際に最も戸惑うのは，省略された式変形と，少し飛躍のある論理の流れであろう．本書は（専門家にとって）名著と呼ばれる古典的な教科書に比べて式変形や説明が各段に丁寧で追いやすく，卒研生にとって読み進めやすい配慮がなされている．
理由4：美文書
テキストやレイアウトはすっきりとしていて，余白も多く，青字も使われていて実にスマート，目にも優しい．図もきれいで，ストレスなく読み進められる．これは，著者だけでなく，出版社の努力も大きいか．
気になる点があるとすれば，後半で扱われている「光学応答」や「半導体」，「超伝導」などの内容は，本格的に固体物理学や物性物理学を勉強しようとする学生には少々物足りないかもしれない．例えば「超伝導」の章ではBCS理論の解説は含まれていない．わかりやすい説明と，面白いトピックスで興味を掻き立てられたのに，いいところで話しが終わってしまった，そんなもどかしい気分になってしまう．もっと知りたい，もっと勉強したいと思った学生はこう考えるだろう．「そうだ図書館で調べてみよう」，「先生，関連する論文や文献を教えていただけませんか？」．教員冥利に尽きる理想の状況，理想の学生である．そこまで含めて，本書は「学部生のための良書」とも言える．本書を読んだ後に，例えば斯波弘行著『基礎の固体物理学』（培風館）や『固体の電子論』（丸善）でさらに学習を深めると効果的かもしれない．ぜひ研究室での学生指導に使ってみたい一冊である．
（2018年8月1日原稿受付）

ページの頭に戻る

非線形光学入門

服部利明

裳華房，東京，2009，xi＋235p，21×15 cm，本体3,800円［専門～学部向］ISBN 978-4-7853-2826-9

紹介者：池田達彦(東大物性研)

物理学会誌のバックナンバーを見返せば明らかなように，高強度レーザーを用いた光物性研究が急速に進展している．関連するキーワードは，ポンプ・プローブ法による電荷やスピンの非平衡ダイナミクス測定，光による超伝導の制御など，枚挙に暇がない．このような潮流の中で，スピン系や強相関電子系，物性基礎などの理論家で，必ずしも光物性のバックグラウンドを持たない研究者の参入が相次いでおり，評者自身もその一人である．近年の高強度レーザーによって初めて測定が可能になった物質の動的側面，特に線形応答を超えた外場への応答が次々と報告される様を目の当たりにし，非平衡物理の新時代の幕開けを予感するのである．
しかし，光物性のバックグラウンドを持たない学生や研究者が最新の実験の原著論文を理解しようとすると，非線形光学現象に関する網羅的な知識の必要性を感じるのではないだろうか．標準的な電磁気学のコースで扱うのは真空中・物質中のマクスウェル方程式と線形応答に限られ，冒頭に挙げたホットトピックスはいずれもその範疇外にあると言わざるを得ない．
本書はこの知識のギャップを埋めるのに最適な，非線形光学のコンパクトな入門書である．第1章では，光波混合や多光子吸収などの典型的な非線形光学現象が線形光学現象と対比して紹介される．また，非線形光学効果を増幅するために極めて重要な位相整合の概念が解説される．第2章と第3章では，それぞれ2次および3次の様々な非線形光学効果が解説される．前者では，第2高調波発生，光整流，光パラメトリック増幅など，後者では，第3高調波発生，光カー効果，縮退・非縮退4光波混合などが取り上げられる． これらは関連する非線形感受率の成分と対応付けて見通しの良い表にまとめられている．3次の非線形光学効果の中でも特に重要な誘導ラマン散乱は， 独立した第4章にて詳細な解説がなされる．最終第5章では一般的で厳密な非線形感受率の定義がなされる．
最終章で一般的な定義が現れるこの型破りな構成は，本書が入門書として非常によく練られていることを端的に示している．前提とされる知識は標準的な学部レベルの電磁気学のみであり， その他の概念は個々の現象の解説の際に必要に応じて導入される．そのため読者は，現象のエッセンスに集中してテンポ良く読み進めることができるし， 徐々に非線形感受率の概念に慣れ，その一般的な定義の深い理解に到達できる．また，解説が全体的に定量的に行われる点も強調したい．数式に飛躍や誤植が極めて少ない非常によくできた教科書である．これらの長所は題材の注意深い取捨選択の賜であり，敢えて省かれた題材については参考文献のリストが添えられている．量子力学は読者層を広げるためにほぼ完全に排除されているが，非線形感受率の導出など， 量子力学を用いた方が理解が深まるであろう部分もある．これらが付録に収録されていれば，より完成度の高い入門書になると思う．
本書は，やや古い本ではあるが，物理系の学生や研究者にとって読み易い非線形光学の入門的な和書は少なく， 光物性や非平衡系に興味がある物理学会員には貴重な一冊である．
（2018年9月1日原稿受付）

ページの頭に戻る

ランダムウォークはじめの一歩；自然現象の解析を見すえて

J. Klafter，I. M. Sokolov著，秋元琢磨訳

共立出版，東京，2018，vii＋178p，22×16 cm，本体2,900円［専門～学部向］ISBN 978-4-320-11324-4

紹介者：金澤輝代士(東工大)

本書はランダムウォークの数理，特にその中でも異常拡散に焦点を当てた入門書である．非常に丁寧に導出・計算が解説されており，初学者に間違いなくお勧めできる内容になっている．また，「通常」の確率過程を知りつつも，「異常」な確率過程には詳しくない者が，異常拡散の分野を速習する上でも役立つ本である．
ランダムウォークと言えば，ブラウン運動などの拡散現象を睨み，移動距離の分散から拡散係数の大きさを測定したりするのが「通常」の定式化である．「通常」の中心極限定理を踏まえて，結果の多くの部分にガウス分布が現れる．更に数理的定式化を洗練すれば，白色ガウスノイズ（ウィーナー過程）に駆動される確率微分方程式を考え，フォッカープランク方程式などを導出する「通常」の確率過程の体系に繋がっていくと思うのが「普通」である．
しかし，上記のような話は「通常」の拡散現象にしか適応できないのも事実である．ここでの異常拡散というのは，典型的にはモデルの一部（ジャンプサイズ分布・待ち時間分布など）にベキ分布が入り込み，その結果として「通常の拡散」と性質が著しく乖離する拡散現象を指す．ここで「通常」と「異常」という表現を持ち出したが，共に自然現象において頻繁に表れることが知られており，その意味で両方とも『自然』な拡散である．
「通常」の中心極限定理の主張を確認しよう．独立同分布に従う乱数列を考えたとき，「乱数の分散が有限ならば，その和は近似的にガウス分布に従う」というのがその主張である．ここで「分散が有限」というのが肝となる条件であり，例えばベキ分布はこの前提条件を充たさない．このような局面では「通常」の中心極限定理が破れ，一般化された中心極限定理が成立する．最終結果に表れる分布はガウス分布とは限らず，一般には安定分布が現れ，それは漸近的にはベキ分布の振る舞いを示す．つまり，ランダムウォークのジャンプサイズの分布がベキ分布に従う場合，最終的な移動距離はガウス分布とは全く異なってベキ分布を示す．
またランダムウォークにおける待ち時間分布を考えよう．「通常」の確率過程ではマルコフ過程を考えるため，待ち時間分布は暗に指数分布であることを仮定する．しかし，待ち時間分布がベキ分布に従う場合を考えると，「通常」のマルコフ過程での枠組みは近似的にさえも正しく現象を記述できず，本質的に異なる拡散現象が観測される．例えば拡散係数を測定しようとしても，そもそものスケーリング関数形が変化する．更にはエイジングと呼ばれる奇妙な振る舞いを系が示すため，そもそもの拡散係数の測定方法に細かな注意が必要になる．
上記のような「異常」な拡散を記述する洗練された数学的定式化はあるのだろうか？　これに対する肯定的な処方箋が本書に体系的に示されている．一般の待ち時間分布に対する一般化マスター方程式・一般化フォッカープランク方程式といった，セミ・マルコフ過程の数理的枠組みで記述することができる．特にベキ分布が前面に現れる時は，非整数階微積分演算子（例えば0.5回微分したり，π回積分したりする演算子）を導入することで，洗練した計算が可能となる．現象解明だけではなく，純粋に数理構造の美を楽しむことが可能な内容になっている．
最後に個人的な感想を述べる．本書評の執筆を依頼される前から，実は本書は筆者のお気に入りであった．特に手を動かして数式を追うことができるように最大限の配慮がされている点に非常に感心した．本書のような応用数学の内容は，結局のところ自分で手を動かし，多数の例題を解かない限り，真の意味では理解することができないと私は思う．その意味では，本書は非常に丁寧に計算が書かれており，初等的な例題から徐々にステップアップして一般化していく形式を取っている．故にきちんとした理解を望む者にも本書は推薦できる．
（2018年9月10日原稿受付）

多波長銀河物理学

A. Boselli著，竹内　努訳

共立出版，東京，2017，x＋320p，23×16 cm，本体8,000円［専門・大学院向］ISBN 978-4-320-04730-3

紹介者：秋山正幸(東北大院理)

物理学会の議論に登場する際に銀河はどう捉えられているのだろうか．宇宙論では銀河はただの質点あるいはテスト粒子としてしか認識されていないかもしれない．しかし，実際の銀河は星，ガス，超大質量ブラックホール，はては暗黒物質からなる複雑系であり，単純な質点と扱うと誤った結論が導かれるかもしれない．
このそれぞれの「点」の物理量を正しく把握するには，多波長の放射の観測から得られる測定量を理解することが欠かせない．例えばガスと一言で言っても，低温の分子ガスは電波での観測が重要になるのに対し，高温の電離ガスはX線での観測が重要になる．さらに銀河のサンプルを構築する際にある波長での放射強度がよく基準に用いられるが，それによってサンプルの物理量がどのようなバイアスを受けて構築されているかの理解も必要だ．本書はまさにこのような銀河のさまざまな測定量を理解し，実際の物理量に結びつけ，サンプルのバイアスを把握するための道しるべを与えてくれる．
銀河の多波長観測はすばる望遠鏡をはじめとする大型の地上望遠鏡や様々な波長の観測衛星の活躍により，私が大学院生だった1990年代後半から飛躍的な発展を遂げた．その成果は様々な波長での測定量のとりまとめから，その物理的理解に至るまで多数の論文として出版されている．複雑系である銀河の研究では，こういった幅広い波長に渡る様々な観測結果と整合性が取れた解釈が求められるが，限られた時間ですべてを把握することは難しい．本書はまさにこの時代の多数の観測成果を，トピックごとに細かく章分けし，議論があり注意を払うべき点に言及しながら良くまとめた辞書のようになっている．
読者としては宇宙天文分野に関わる研究者やそれを志す大学院生が想定されるだろう．本書の数式での記述は限定的で，経験則から得られた関係式と物理原理から導かれる関係式が混合して登場するので，そこは読者が注意を払う必要はある．本書が豊富に示すリファレンスは，原論文に戻り，それぞれの式が導き出された観測手法や背景を理解し，最新の研究成果へとつながる良い糸口を与えてくれる．
原著の表現を厳密に踏襲しようとしたためか，日本語としてこなれない部分があり，やや読みにくいかもしれない．また初版では誤字も散見される．しかし，訳者により付けられた多数の注釈はそれをおぎなって余りある魅力があり，研究の最新の動向の補足だけでなく，研究者の人間模様まで垣間見えるコラムのような役割を果たしている．銀河をテスト粒子とするにしても，ぜひ手元にあると良い「辞書」になるのではないだろうか．
（2018年9月20日原稿受付）

ページの頭に戻る

電気回路と伝送線路の基礎

阿部真之，土岐　博

丸善出版，東京，2017，xi＋229p，21×15 cm，本体2,600円［学部向］ISBN 978-4-621-30206-4

紹介者：前田順平（神戸大理）

本書は，回路理論や伝送理論と電磁気学との関係性に主眼を置いて，体系的に述べることに重点を置いたものである．工学系の回路理論の教科書と，理学系のマクスウェル方程式等を学ぶ電磁気学の教科書では，それぞれ独立に記述されている書籍は多いが，本書はその接続を分かりやすく行い，お互いの橋渡し役になっている．
全11章中の前半6章は回路理論について丁寧に説明されている．理解に必要な数学の知識や，基本的だが他の教科書ではあまり説明されていないことまで触れており，本書だけであっても十分学修できるものと考えられる．物理学を専攻している学生にとっては，あまり回路理論について学ぶ機会がない者も多いだろう．そういった人には，他の回路理論に特化した教科書に比べれば，理解しやすいものとなっているのでぜひ目を通してもらいたい．
7章ではマクスウェル方程式について説明しており，物理学科の学生にも馴染みのある一般的な電磁気学の教科書となっている．その後8章「マクスウェル方程式から導出した伝送線路理論」以降からいわゆる電磁気学と伝送線路の理論を結びつけている．物理学科が行う電磁気ではあまり手の届かない分野である一方，例えば最先端の素粒子実験では避けて通れない分野であり，前半で挫折した人にも，ぜひ7章から再び読み進めてもらいたいと思う．最後の電磁ノイズに対する解説まで一通り基礎を学ぶには最適な教科書であるが，もう少し具体的な実践例を挙げても良かったと感じた．本書の著者の一人である土岐氏は，J-PARCにおける電磁石電源の電流リップルによる影響を抑えることに成功したことでも知られている．1ページ程度のコラム等で良いので，本書の内容がどのように応用されているかを紹介しても良かったのではないかと感じた．
また工学系の教科書にはよく見られるが，理学系の教科書では不足していることが多い数値計算に重きを置いている点や，グラフを可視化している点は良かった．最近流行りのPython言語で記述したソースを付録としてウェブページで提供しているので自己学修には助かるであろう．一方，本書中でそのPythonに触れている部分が中途半端であり，ソースコードの類はむしろ全てウェブページに任せてしまった方がまとまり良く収まったかもしれないと感じた．
基礎から電気回路，特に分布定数回路を意識させるという点で，電気工学系の学生に限らず，物理学実験で電子回路を開発する必要のある大学院生にもぜひ一読してもらいたい良著である．
（2018年9月12日原稿受付）

ページの頭に戻る

量子流体力学

坪田　誠，笠松健一，小林未知数，竹内宏光

丸善出版，東京，2018，vii＋338p，21×15 cm，本体5,000円［専門～学部向］ISBN 978-4-621-30247-7

川口由紀（名大院工）

低温で量子凝縮を起こした流体は，容器の壁面との摩擦がなく無散逸で流れるという超流動性を示す．これは，流体が単一の波動関数で記述できるという量子性の帰結であり，流体の流れは波動関数の勾配に比例したポテンシャル流となる．このような量子流体力学は，古くは1940年代の超流動ヘリウム4の熱対向流の研究に始まり，超流動ヘリウム3や冷却原子気体のボース・アインシュタイン凝縮体（BEC）と舞台を広げて研究されてきた．その一番の特徴は，渦の量子化，すなわち渦が連続的にできたり消えたりしないという性質である．特に，近年，超流動ヘリウム4や原子気体BECにおいて，量子渦が直接的に可視化されるようになり，その動力学の研究が活発になってきている．量子流体は，一見，古典的な流体とは大きく異なる性質を持つように思われるが，速度差のある2流体の界面が波状に変形するKelvin-Helmholtz不安定性や，Kolmogorov則と呼ばれる乱流に特徴的な統計則など，古典流体で知られた現象が量子流体においても起こりうることが近年の研究でわかってきた．量子流体を利用すれば，これらの現象における渦の役割を微視的な観点から解明することができるとして，古典流体との対応も注目されている．本書はこのような量子流体・量子乱流の研究を長年，第一線で行ってきた著者らによるもので，量子流体力学として初めての教科書である．
本書の第1章は，量子流体の基本概念および様々な量子流体の紹介から始まる．第2章ではより具体的に，量子統計や，素励起，自発的対称性の破れといった概念が導入されたのち，超流動ヘリウム4，超流動ヘリウム3，原子気体BECのそれぞれに対し，特徴や定式化が述べられる．個々の系について詳しく説明すると膨大な量になってしまうが，ここでは本書の後半を読み進めるのに必要最低限の内容がコンパクトにまとめられている．第3章以降が本題の量子流体力学となる．第3，4章では量子渦の性質に関して，超流動ヘリウムと原子気体BECのそれぞれについてまとめられている．量子渦糸の基本的な運動や，その数値シミュレーション方法，内部自由度を持つ系における渦の分類，実験での渦生成観測方法など，量子渦に関する事項が網羅的に述べられている．第5，6章は流れの不安定性，および乱流現象という古典流体で知られた現象を量子流体の観点から議論している．単なる粘性ゼロの古典流体でなく，量子性に由来する不安定性や量子渦の運動が議論できる点が興味深い．第7章はブラックホールや中性子星，液晶など他の系と量子流体との類似性について述べられた後，まとめと展望で締めくくられる．
本書の最終章でも述べられているが，本書の内容は量子凝縮系を流体力学の観点から非平衡統計力学の理論と結びつけた研究領域にあたる．このような学問領域に興味のある読者にはもちろん，量子渦や超流動現象を学びたいと考える学生の入門書としても薦めたい一冊である．
（2018年10月3日原稿受付）

ページの頭に戻る

固体電子構造論；密度汎関数理論から電子相関まで

藤原毅夫

内田老鶴圃，東京，2015，ix＋233p，21×15 cm，本体4,200円（物質・材料テキストシリーズ）［専門～学部向］ISBN 978-4-7536-2302-0

石井史之（金沢大ナノマテリアル研究所）

パソコンがひと昔前のスーパーコンピュータの計算能力を持っている，と言われるようにコンピュータの計算能力の向上が著しい昨今である．複雑な系の電子構造が低コストで計算できるようになり，密度汎関数法に基づく第一原理計算（凝縮系の電子構造計算）が，研究手法として広く普及している．評者が学生だった頃（1990年代後半）にはインターネット上で公開されていた計算プログラムの数は極僅かであったが，現在では数多くの計算プログラムが公開されており，ダウンロードして利用することができるようになった．*
主に専門家とその研究室の学生のみが行っていた電子構造計算が，他に専門を持つ多くの研究者によっても行われ，研究において欠かせない要素となってきており，凝縮系物理学の基礎知識として固体電子構造論を学ぶ重要性はますます高まっている．以前と比べると，「教科書には載っていない」知見がインターネット上で共有されるようにはなってきたが，情報のまとまった書物の重要性は高い．また，計算結果の妥当性をチェックするためにも，固体電子構造論への深い理解が不可欠である．本書の著者の目指すところは，若い研究者や学生の「電子構造計算の方法論開発への意欲を刺激し，そして電子状態計算理論全体を俯瞰的に眺める」ことに役立てることであるが，多くの電子構造計算に携わる研究者にとっても有用であると思われる．
本書は1999年に出版された『固体電子構造―物質設計の基礎―』（朝倉書店，1999年）が全面的に改訂されたものである．1章から3章までで，周期系の多電子問題を解く密度汎関数法の説明とその準備に費やされ，4章で一電子問題を解くための種々の方法が説明され，5章，6章と金属，半導体への応用が示されている．7章は新たに追加された章であり，近年のトポロジカル物質の研究で，その重要性が一段と高まったベリー位相について，「電子バンドのベリー位相と電気分極」として説明されている．8章は物質設計の手法として重要性の高い第一原理分子動力学法の説明にあてられている．9章は旧著では3章に含まれていた部分であるが，独立してより詳細に「密度汎関数理論を超えて」として，自己補正相互作用，LDA＋U法，GW法，量子モンテカルロ法，動的平均場理論（DMFT）など，密度汎関数法でバンドギャップが過小評価される問題や，強相関電子系へのアプローチが紹介されている．他に，新たに書き加えられている事項を並べると，時間依存密度汎関数法（応答関数の計算），密度汎関数摂動論（フォノン分散の計算），PAW法，LMTO法に関する発展，オーダーN法（クリロフ部分空間法）などがある．また，シュレディンガー方程式の解法等，数値計算の技術的な諸問題に関しては改めて付録にまとめられ，自分でプログラムを作成したい読者や詳細を知りたい読者にとっては有用な付録となったと思われる．
以上のように，本書は，電子構造計算をはじめる人が，多くの計算技術について，何から勉強してよいか判らないときに，「電子状態計算理論全体を俯瞰的に眺める」ための良いガイドとなるであろう．また，より深く理解するために，各方法論の原著論文を読む前に概観をつかむのにもよいであろう．多くの研究者に一読することを勧めたい一冊である．

*例えば次のサイトによくまとめられているhttps://ma.issp.u-tokyo.ac.jp
（2018年11月16日原稿受付）

ページの頭に戻る

本質から理解する数学的手法

荒木　修，齋藤智彦

裳華房，東京，2016，viii＋200p，21×15 cm，本体2,300円［学部向］ISBN 978-4-7853-1570-2

小鍋　哲（法政大理工）

理工系学部低学年の学生は，限られた時間の中で幅広い分野の数学を学ばなければならないため，その数学を何のために学ぶかをわからないまま，概念の本質を十分に咀嚼する余裕もなく，計算技術の習得ばかりに関心がいってしまいがちである．そのため，なんとなく計算問題はできるが，本質がわかった気がせずモヤモヤしたまま，という学生も多くみられる．そのような中，本書は，理工系学部1・2年生を対象にした基礎数学の教科書として，「学ぶ意義は何か」，「本質は何か」，「何の役に立つか」という問題意識を全面に出し，理工系の学生にとって理解しにくい，もしくは理解したつもりになりがちなテーマについて，軽快な語り口調で丁寧に解説している．
本書は，第1章で，数学を学ぶ上での心がけや基礎知識について説明したあと，第2章から第9章までは，それぞれ異なるテーマについてほぼ独立した形で解説している（取り扱っているテーマは，第2章：「テイラー展開」，第3章：「多変数・ベクトル関数の微分」，第4章：「線積分・面積分・体積積分」，第5章：「ベクトル場の発散と回転」，第6章：「フーリエ級数・変換とラプラス変換」，第7章：「微分方程式」，第8章：「行列と線形代数」，第9章：「群論の初歩」となっている）．そのため，第2章以降は，読者の興味や必要性に応じて好きな章を読むことができる．各章のはじめにその章で扱うテーマの目的や本質が何であるかを簡潔に述べ（例えば，第2章の「テイラー展開」では，"「計算が複雑過ぎてやばい！」という数式に出会ったとき，真っ先に試すべきはテイラー展開である．テイラー展開は，どんな微分可能な関数でもべき関数の和という簡単な式に置き換えてくれる道具である"，と始まる），その後，直感に訴えかける図を活用し，詳細かつ明快な解説をしている．そのため，読者は，ゴールを見失うことなく安心して読み進めることができる．軽快な解説もさることながら，随所に盛り込まれている著者S先生の数学に関するユーモアあふれる思い出エピソードが，読者を飽きさせない（S先生の思い出ばなしや告白に共感する読者も多いのではないだろうか）．また，出版社のホームページには，各テーマについての演習問題が詳しい解答とともに掲載されているので，理解を深める上で大変役に立つだろう．
本書は，教養基礎数学の理解を目的としているため，取り上げているテーマはスタンダードなものである．しかし，学ぶ目的を明確にし，本質を捉えた解説がふんだんに盛り込まれた本書は，初学者がより深く数学を理解するため，また，基礎数学を教えている教員の講義用として，さらには，モヤモヤしたままの学部高学年生や大学院生（もちろん，研究者や技術者）にとっても，極めて有益な本となるに違いない．学生たちを「なんとなく理解したつもり」にさせないためにも，私の講義では早速本書を参考書として活用させていただく．
（2019年1月15日原稿受付）

ページの頭に戻る

熱電材料の物質科学；熱力学・物性物理学・ナノ科学

寺崎一郎

内田老鶴圃，東京，2017，ix＋242p，21×15 cm，本体4,200円（物質・材料テキストシリーズ）［専門～学部向］ISBN 978-4-7536-2311-2

高畠敏郞（広島大院先端物質）

熱電変換は廃熱の有効利用だけでなく，最近では，各種センサーの自立型電源への応用が盛んに研究されているので，本書の出版は時宜を得ている．副題の「熱力学・物性物理学・ナノ科学」に表されているような，物性物理学の基礎から熱電材料までを一人で書いた初めての日本語の教科書である．H. J. GoldsmidによるIntroduction to Thermoelectricityに比べて本書は物理的洞察に富むので，英語版が出版されることを強く望む．著者の博覧強記と教育的配慮が至るところに発揮されていることに私は魅了された．特に，授業中に語りかける調子での書きぶりは，ハードルを下げている．それでいて，各節の書き出しは，格調高く簡潔である．例えば，「半導体がエレクトロニクスの基幹材料となった理由は，不純物ドーピングという物性制御法にある．」は，著者ならではの表現かと思う．
全8章のうち，1～5章は基礎であり，6～8章に有望な熱電材料とナノ構造化による性能向上がまとめられている．それぞれ，下記のような特徴を持つ．第1章では熱電変換について概説した後，その応用分野を述べ，効率を太陽光発電などと比較している．第2章では，熱電係数を導いた後に，熱力学に基づいて熱電素子の変換効率を求め，適合因子の重要性を述べている．第3章の「固体の電子論」は，1次元系で説明した後に3次元系に移るという手法で，バリアーを下げている．読者が戸惑う個所には，「蛇足ながら」の後に説明を加えている．ただし，フェルミ-ディラック分布関数についての参考書としては，日本語の教科書が望ましい．第4章はフォノンによる熱伝導までを簡潔にまとめてある．第5章では，金属と半導体における電子の散乱とフォノンの散乱について記述している．その中で，図5.2は分かりやすく工夫されている．秀逸なのは，著者独自の方法でKelvinの公式を導出している点である．5.6節の設計指針を読めば，1～5章までの内容を読者がどの程度理解したかを自己採点できる．
第6章では有望な熱電変換材料として11種類の例を挙げて，その特徴と問題点を述べている．問題の捉え方に著者の物理的センスが現れている．材料の多元系化合物への展開の起源を1986年の銅酸化物高温超伝導体とし，有機伝導体の欠点を移動度の低さとするところに，著者の研究歴に基づく物質観が窺われる．第7章の前半では，著者が取り組んできたCo酸化物の熱電物性を紹介している．従来の縮退半導体とは異なり，軌道とスピンのエントロピーがゼーベック係数を高めているという強相関系物理のエッセンスが説明されている．一方，高温超伝導体Cu酸化物は軌道とスピンの自由度が無いので，熱電材料には適さないことがさらりと記述されている．中間の7.3節では重い電子系が低温で高い出力因子を示す理由が示されている．話の順番としてCu酸化物の記述をCo酸化物のすぐ後につなげた方が，読者に分かりやすいと思う．第8章では，Nature誌とScience誌に華々しく登場した「ナノ構造化による飛躍的な性能向上」のどこが怪しいかをチクリと指摘している．最後に，スピンゼーベック効果への期待が述べられている．
以上のように，本書を最後まで読めば，熱電変換の物理から材料開発の最前線までを理解できた気がする．刺激を受けた読者が，新しい原理による熱電変換材料を創製することにつながるであろう．
（2019年1月29日原稿受付）

ページの頭に戻る

基幹講座物理学　量子力学

益川敏英監修，植松恒夫，青山秀明編集，国広悌二著

東京図書，東京，2018，xiv＋337p，21×15 cm，本体3,500円［専門～学部向］ISBN 978-4-489-02294-4

土手昭伸（KEK理論センター）

量子力学は今日どの分野でも当然の道具として使用され，物理学を学ぶ者にとって必修の科目である．本書は，学部学生を対象とした量子力学のテキストである．近年，特に学部生向けテキストは大変分かり易く工夫されたものが多い．私が学生の頃と比べると行間が広く，図が多用され，中にはカラフルなものもある．本書は一見，このような昨今の風潮に逆行している．しかし忍耐強く読むと実は懇切丁寧な説明がなされている．まさにシリーズ監修者（益川氏）による前書きにあるように，「各ステップを読み解くことで完全な理解が得られる」テキストである．
本書の構成は以下の通りである．量子力学へ至る過程（1章）から始まり，2～4章で量子力学の一般的枠組みが，主に1次元ポテンシャルを用いてじっくり説明される．続く5章にて2，3次元ポテンシャルでの束縛状態について，シュレーディンガー方程式の解法が具体的に示される．6～10章では回転など各種変換，更にはゲージ変換，これらに伴う対称性の話が続く．11～13章で摂動論や変分法などシュレーディンガー方程式の近似的解法，14章ではハートリー・フォック法やフェルミガス模型など同種粒子からなる量子多体系の取扱い方が述べられている．最後の15章では量子統計について簡潔に説明されている．途中，調和振動子ポテンシャルでの生成消滅演算子や角運動量代数も詳しく説明されており，量子力学を学ぶ上で必要不可欠な基礎的事項をほぼ全てカバーしている．各章の終わりに，その章の内容を掘り下げた，あるいは延長上にある問題が用意されており，とても教育的である．なお巻末にはそれらの解答がコンパクトに，また必要に応じて詳しく与えられている．
多分に私見になるが，本書の特色を述べておく．確かに一見無骨な体裁であるが，実は計算の詳細まで書かれている．3章や5章では，ベクトル解析や特殊関数について物理数学のテキスト並みに説明されており，ほぼself-containedである．大学院入試を控えた学生にとっては，計算の良いトレーニングになるだろう．数式が文章中に埋め込まれていて見難い部分もあるものの，逆にコンパクトで巧みな文章によってリズミカルに話が展開されている．11章のRayleigh-Schrödinger型摂動論の説明は，基本的にはJ. J. サクライのテキストなどと同じだが，最初にこの摂動論に現れる線型方程式の構造を整頓しておくことで，その後の説明が見通しよくなっている．計算だけでなく何事も順を追って丁寧に説明されている．用語の定義に注意を払い，慎重に言葉を用いて厳密な説明を心がけている．その際豊富に引用されている古典的名著も，読者にとって良いガイドとなろう．また端々で著者らしいユニークな言い回しがある．例えば "...多彩な物理的効果が生まれる．すなわち「創発される」．"（14章冒頭要旨）．端的に本質を突いた表現が印象的である．また低エネルギー中性子散乱でのvirtual state（2.11節），素粒子・原子核物理で重要なカイラル対称性（8章脚注）など，所々で挿入されているアドバンストな話題は学生の興味を刺激するであろう．ただ1章最後の節は，脚注にもあるように，幾何光学と解析力学について十分な知識がないと理解が難しい．この部分は昨今の分かり易いテキストを片手に読むか，時間のない学生は深入りしなくてもよいように思える．
本書は学部学生を対象に想定しているが，大学院生・ポスドクそして現役の研究者の方たちにも勧めたい．私もそうだが日々当たり前に量子力学を使っていると，つい見落としている点がある．3.3節での演算子のエルミート性の話など，改めて自分の足元を見直す話が多々あった．また摂動論（11章）の中で，散乱問題を扱うLippmann-Schwinger方程式，更にはその核媒質中版であるBethe-Goldstone方程式に言及している．ハドロン・原子核分野でお馴染みのこれらの方程式がBrillouin-Wigner型摂動論と形式的に同じといった記述は興味深く思えた．このように中堅・シニアにとっても有益な話題が随所に散りばめられている．
最後に．本書は必ずしも学生に対してフレンドリーではない．しかし研究者を志す若者には頑張って読んで欲しい．なぜなら学問は容易ではなく，努力した者に対してのみ微笑む．本書を通じ「学問に王道なし」を味わえるのではないだろうか．
（2019年2月4日原稿受付）

ページの頭に戻る

走査透過電子顕微鏡の物理

田中信夫

共立出版，東京，2018，viii＋161p，21×15 cm，本体2,000円（基本法則から読み解く物理学最前線20）［専門・大学院向］ISBN 978-4-320-03540-9

高山あかり（早大先進理工）

最近，故あって電子顕微鏡のセミナーを主催してほしい，という依頼を受けた．とはいえ，光電子分光が専門の私には，電子顕微鏡というと，「走査電子顕微鏡（SEM）」と「透過電子顕微鏡（TEM）」の浅い知識しかないという状態である．幸い，セミナー自体は運営委員の先生方のおかげで無事に開催され，私自身，豪華な講師陣から電子顕微鏡を学ぶ良い機会となった．恥を忍んで打ち明けるが，そこで初めて「走査透過電子顕微鏡（STEM）」というものが存在することを知り，もう少し深く理解したいと思っていた矢先，本書を見つけた．この「基本法則から読み解く物理学最前線」シリーズは，最新の物理トピックスを各巻1つずつ取り上げ，基礎から最先端の研究までを幅広く紹介している有難いシリーズである．私自身，本書以外にも愛読している分冊がいくつもあり，これは良いと手に取った次第である．
本書は，走査透過電子顕微鏡について，その原理，装置開発の歴史，最新の研究例まで，幅広い内容を取り上げている．
1～2章では，「どうやって原子を見るか」という導入で，電子顕微鏡でどのように原子が見えるのかを歴史とともに紹介されている．DNAに付着したウラン単原子における世界初のSTEMによる単原子観察から始まり，現在では窒化ホウ素のホウ素と窒素の識別，最も軽い元素である水素の観察も可能になったとは驚きである．
3～4章では，どのように電子顕微鏡像を得るのか，という点を光学顕微鏡との対比も交えて紹介されている．特にSTEMの場合，電子線をSTM探針のように走査する必要がある．どのように電子ビーム径を細くするのか（ボケが生じる原因は何か），どうやって走査するのかの基本が説明されている．
本書のメイン，STEMにおける結像の原理や各種結像モードは5～6章で取り上げられている．単結晶試料に電子線プローブを入射する場合のSTEM像は，①多数の平面波で合成された入射プローブが単位胞のどこに入射するのか，②有限の厚みをもつ試料において入射プローブが結晶内でどのように回折されるのか，③観測された収束電子回折図形のどの部分の強度を検出するか，の3ステップで決まる．また，最近のSTEMは，検出器や収束電子回折図形の解析方法を工夫することで，単純な暗視野像・明視野像だけではなく，様々な情報が得られるようになっている．STEMを用いた原子周りの局所電場や磁場の測定（しかも原子スケール！），3次元観察もすでに達成されており，これらの最新研究についても丁寧に説明されている．
最後の7～8章では，STEMの実際の装置や分解能を上げるための技術や工夫などが述べられており，本書を1冊読むと，奥深いSTEMの表面だけではあるが，概要をひととおり学ぶことができた．
本書は，実験ハンドブックというよりはSTEMの基礎的な原理を中心にまとめられているため，大学や企業で初めてSTEMを使う人がその原理を学ぶには最適な本であると思う反面，大学1～2年生には少々難しい内容となっている．特に，固体物理の基礎的な概念，数学的知識（中でもフーリエ解析）は本書を読む上で非常に重要な要素を占める．本書にも付録として説明がなされているが，より深く理解するには，物理数学や固体物理学の教科書とセットで学ぶと良いだろう．とはいえ，本文125ページ，付録18ページの中に電子顕微鏡のエッセンスを凝縮して書かれた本書はSTEMの入門書としては最適である．STEMを扱う方，興味のある方は是非本書を読んでいただきたい．
最後になるが，本書で20冊目となるこのシリーズ，取り上げられていないホットトピックはまだまだある．監修・執筆者の先生方に感謝するとともに，今後の刊行も非常に期待したい．
（2019年2月1日原稿受付）

ページの頭に戻る

新版X線反射率法入門

桜井健次

講談社，東京，2018，xiv＋369p，21cm×15cm，本体6,300円（KS物理専門書）［専門・大学院向］ISBN 978-4-06-153296-0

和達大樹（東大物性研，兵庫県立大院物質理）

X線反射率法は，薄膜などの物質の深さ方向の情報などを得る実験手法としてすでによく確立しているが，まとまった教科書は意外と少ない．これには様々な理由が考えられるが，大きな理由の一つとして，X線反射率法から得られる情報が，薄膜の膜密度，膜厚，表面界面の粗さから，ひいては共鳴磁気反射率によるスピンの状態に至るまで非常に多岐にわたることが挙げられる．21世紀に入り，ナノテクノロジーの急速な発展によりX線による表面界面計測がさらに重要となっている．また，X線自由電子レーザーの登場により，レーザー分野との融合も急速に進んでいる．このような流れの中，スタンダードなX線反射率法の教科書が待ち望まれてきた．
本書は，X線反射率法の基礎原理に始まり，得られたデータの解析法，そして豊富な適用例と周辺分野の紹介まで，体系的にカバーした本格的な教科書である．韓国語にも翻訳されるなど，世界の研究者にとって入門書となっている．私自身はX線反射率法よりむしろX線（特に軟X線）の光電子分光や吸収分光などの分光測定をバックグラウンドにしてきたが，本書からX線反射率法について多くを学ぶことができた．このようなことから，本書は物理学会会員の方々にも有用な書籍と思われる．なお，本書は2018年に発行された新版であり，旧版は2009年に発行されている．改訂により，第五，六章の空間・時間分解，第九章の中性子などが加わり，研究の新しい流れや研究分野の融合がより強く感じられるようになった．
本書は，第一章のX線反射率法の基礎から始まる．X線領域の物質の屈折率が1よりやや小さいことの説明から，薄膜の膜密度，膜厚，表面界面の粗さなどがどのように決まるかが述べられている．磁性体に対する共鳴磁気反射率やコヒーレント回折も言及されている．第二章はX線反射率測定法の測定装置と測定方法である．X線の単色化や検出器についてはかなり詳しく説明されている．この第一，二章は私がX線領域の光物性物理学の大学院講義を行う際に非常に参考となった．
第三，四章はX線反射率測定のデータ解析である．第一章で出てきたParrattの漸化式などが具体的に適用されている．旧版では巻末にC＋＋での計算プログラムがあったのだが，これは講談社のホームページからダウンロードできるようになり，さらに便利になった．
第五章はイメージングへの展開であり，ゾーンプレートやKBミラーによる微小ビームを用いた方法と，ビームを絞らない画像再構成法が述べられている．第六章は時間分解測定であり，動作下（オペランド計測）による機能の研究が述べられている．第七章はX線反射率法の応用例であり，半導体薄膜やハードディスクから電気化学界面などの固液界面までが含まれている．第八，九章は周辺分野であり，軟X線，小角散乱から中性子までが述べられている．
X線反射率法において，基礎原理から始めてここまで網羅的にカバーした教科書は類を見ない．本書は，前半は分野外の研究者にも十分理解でき，学部後半から大学院講義にもふさわしい．その一方，X線の研究室に入った学生や若手研究者にとっては通読しておくべき価値がある．磁性体に対する研究は，第一章の共鳴磁気反射率の部分などに限られており，これについては例えばJ. Stohr and H. C. Siegmann, Magnetism: From Fundamentals to Nanoscale Dynamics（Springer, Berlin, 2006）などがXMCD（X-ray Magnetic Circular Dichroism）に詳しく，相補的である．
次の新版ではX線自由電子レーザーの短パルス性やコヒーレンスを用いた研究が述べられるのだろう，という大きな発展性を感じられるのも本書の魅力である．
（2019年1月22日原稿受付）

ページの頭に戻る

分子エレクトロニクスの基礎；有機伝導体の電子論から応用まで

森　健彦

化学同人，京都，2013，viii＋461p，22×15 cm，本体9,500円（DOJIN ACADEMIC SERIES）［専門・大学院向］ISBN 978-4-7598-1414-9

廣部大地（分子研）

研究室に配属されるやいなや，はじめて触る物質を用いて聞いたこともない現象を調べることとなるのは常である．先行論文にあたるも，データや式の読み方がわからないという苦い思いは誰しも経験があるだろう．また，どうやって目的物質をつくるかという課題にも直面する．ここにきて，「教科書以降，専門書以前の基本をまずは直観的に押さえる」という必要性がでてくる．有機物を題材としてこの要請にこたえるのが本書である．本書の主眼は有機伝導体であり，その基礎事項を物理と化学の双方から解説する．まえがきにもあるとおり，目標は「新物質の性質を明らかにしたり，これから新物質を開発するために必要な知識を得る」ことにある．ここでいう物質とは，電荷移動錯体や有機半導体と呼ばれる物質のことである．前者は第七章，後者は第八章で取り扱われる．これらを理解するための基礎が第一章から第六章であたえられる．
第一章は量子化学であり，主題は分子軌道法である．もっとも単純な例としてHückel法を導入して様々な分子に適用する．これにより，分子軌道をもとめる手続きに慣れてゆく．また，二重結合の共役をもつ環状の分子であっても，かならずしも非局在化エネルギーの利得があるわけではないこと（Hückel則）を学ぶ．第七章で種あかしがあるように，この知見は有機伝導体中のよいドナーとアクセプターをつくる指針となる．第二章では，強結合近似および自由電子近似というおなじみの近似法と分子軌道法との関連性が説かれる．個人的に興味深かったのは，強結合近似によるHückel則の説明であり，ベンゼン環を例とする環状π電子系の安定性をエネルギーバンドの範疇で理解可能だとわかる．中盤以降は輸送現象に向けた下準備として，エネルギーバンド理論とフェルミ分布関数を概説する．有機伝導体の開発という視点から，Peierls不安定性とその原因がフェルミ面の低次元性にあることを指摘しており，電気伝導の観点から二次元以上のフェルミ面が望ましいことがわかる．第三章と第四章ではそれぞれ輸送現象と磁性が扱われる．内容は修士が学ぶ標準的な教科書ほどである．第五章と第六章は電子相関と超伝導の解説に割かれる．磁気秩序や超伝導といった異なる現象の多くがHubbard模型とその拡張で把握でき，ときに平均場近似にあらわれる秩序変数の違いとして統一的に理解できることをみる．さいごに前章までの伏線を回収し，有機伝導体の各論として第七章と第八章が展開される．取っ掛かりとして，第七章のはじめに有機伝導体の設計指針が示される．有機伝導体の条件をπ系の空間分布の立場から直観的に述べ，そのような電子分布をもつ分子の酸化還元をHOMOとLUMOのことばで整理してゆき，さいごに化学修飾と6π系の重要性を説く．ここまでくれば，高伝導の有機電荷移動錯体の設計のあらましがわかるだろう．つづく具体的な物質群の各論は，各自の興味にしたがって拾い読みするのに適している．
有機伝導体分野の鳥瞰図として，これから研究をはじめる化学・物理系の大学院生や研究者におすすめしたい．
（2019年1月31日原稿受付）

ページの頭に戻る

物性物理のための場の理論・グリーン関数；量子多体系をどう解くか？

小形正男

サイエンス社，東京，2018，v＋222p，26×18 cm，本体2,500円（SGCライブラリ-142）［専門・大学院向］ISSN 4910054700688

山地洋平（東大院工）

物性物理学に現れる多体問題に挑むための理論的手法は多岐にわたります．本書の著者は，量子多体系の波動関数を直接用いる理論手法に多大な貢献をされており，著者による解説記事（日本物理学会誌49（11）, 893（1994））は多くの会員が読まれたのではないでしょうか．波動関数法は非摂動的である一方，有限粒子系に適用が限られ（行列/テンソル積表現は例外ですが），有限温度や有限周波数での線形応答の計算には未だに困難があります．
他方，古くから用いられてきた多体粒子系の情報を圧縮する手法の一つが，グリーン関数の方法です．ハイゼンベルク描像の演算子の積（相関関数）に対する（虚）時間発展方程式のグリーン関数を，種々の時間方向の境界条件に対して求め，量子多体系を記述します．自由粒子系のような解ける系のグリーン関数を使って摂動論によって対象系を計算するのが常套手段です．
グリーン関数の方法は有限温度の扱いや線形応答係数の計算を可能とする一方で，境界条件や積分計算における積分経路の取り方にはコツがあり，それらを習得するにはアブリコソフ-ゴリコフ-ジャロシンスキの場の量子論のような専門的な教科書を読んで修行を積まねばと思わされます．また，どうやって観測量を式に落としこむか，近似の妥当性を保証するかなど，理論計算を統御する力が求められます（多々良源博士著の『スピントロニクス理論の基礎』（2010年8月号新著紹介）ではこのコツに焦点が当てられています）．
本書は，波動関数法にとどまらず，場の理論やグリーン関数を用いた量子多体系の研究を近年精力的に展開している著者による，グリーン関数を用いた線形応答計算に力点を置いた大学院生向けの教科書です．まず，第一量子化と第二量子化の関係が簡潔かつ明解に記述され，本書で扱われる多体系のハミルトニアンが導入されます（1, 2章）．グリーン関数の導入（3章）後，摂動論と線形応答理論（4,5章）に続き，電子ガスにおける誘電応答や準粒子寿命（6章），ハバード模型における自発的対称性の破れ（7章），不純物散乱を含む輸送係数（8章）や電子格子相互作用（9章），ならびに超伝導（10章）など，幅広い重要テーマを題材に，前述のコツや難しさがコンパクトかつ明解に記述されています．電子ガスは長い歴史のある話題ですが，第一原理電子状態計算と格子模型研究の合流が進む現在，双方の基礎として，より一層大事な教材となってきています（高田康民博士著の『多体問題』（2000年8月号新著紹介）とその続巻もあわせてご覧ください）．また，本文に収まらなかった話題や式展開については，充実した演習問題が補っています．
本書の特色として，著者の研究と密接に関連する古くて新しいテーマである異常ホール効果やその背後にあるベリー位相（8章），熱輸送（11章），および軌道帯磁率（12章）が紹介されていることがあります．これらの解説はトポロジカル超伝導体や量子スピン液体などを特徴付ける量として注目されている熱ホール係数の計算などへの導入にもなっています．熱についての線形応答は古くから研究されてきた一方，どのように計算するかについては対象系ごとに注意が必要であり，未だ研究が続いていることを本書は伝えています．例えば熱流の計算では，通常の電荷輸送とは異なり，ラッティンジャー考案の仮想的な重力ポテンシャルへの応答のような工夫が必要となるため，系を記述するハミルトニアンに応じて熱流演算子を注意深く求めなければならないことを教えてくれます．注意を要するテーマを取り扱っていることを反映し，類書では見過ごされがちだった問題にも触れています．温度グリーン関数から実周波数へ解析接続する際の一意性についての明解な議論（3章）や，熱輸送や軌道帯磁率の定式化において厄介な問題となる座標rの演算子の取り扱い（8章）がその例です．
本書では多くは語られなかった多体ボース粒子系や運動方程式の切断近似について，著者がどのように記述されるのか，是非読んでみたかったなと思いながら筆を置かせていただきます．
（2019年1月23日原稿受付）

ページの頭に戻る

講談社，東京，2018，xiv＋321p，21×15 cm，本体3,600円（今度こそわかるシリーズ）［大学院向］ISBN 978-4-06-511501-5

糸山浩司（阪市大院理・NITEP）

本書『今度こそわかる重力理論』の著者和田純夫氏は素粒子理論研究者であり，近年は電磁気学，波動等の学部レベルの教科書や一般向け書物を数多く著しておられる．評者も素粒子理論・場の量子論研究者であり，一般相対論を講義したのは帰国直後の二十数年以上前に遡る所謂nonexpertであるが，これもまた会誌編集委員会の意向であると考えお受けすることにした．丁寧に読んだつもりである．
多くの一般相対論の教科書は，等価原理と一般座標変換に対する共変性に始まり，リーマン幾何学を展開する．Einstein方程式を得た後，典型的な応用（惑星問題とブラックホール，重力波，宇宙論）を述べ終わっている．本書もまた，1章から7章までと10章の一部に関しては大筋その流れに沿っているが，リーマン幾何学としての側面は抑え気味に書かれている．その代わりというと語弊を招くかもしれないが，ベクトル場のゲージ理論である電磁気学にしばしば言及し，この場合を雛形として読者をEinstein方程式に導こうと試みている．変分原理，Euler-Lagrange方程式を説明する等，教育的配慮もいくつか見受けられる．この系列の教科書で評者がすぐ思いつく有名な本としては，参考文献に引用されているS. Weinberg "Gravitation and Cosmology"が挙げられるだろう．
8章以降は，著者の過去の重力場研究の基本部分（正準形式とその量子化，量子宇宙論の初歩）をまとめたものと，最近の進展を手際よくまとめた部分（修正重力理論と有質量重力理論）からなるとの印象を持った．昔からあるスカラー・テンソル理論の記述も含まれている．現代の重力場研究のフロンティアを大学院生の前にさらすことを目標に掲げた大胆かつ挑戦的な本であると判断した．
本書は重力の本であるので，古典化された対象を取り扱う学問への教科書である．しかしながら物質の微視的構造は量子論により与えられ，重力といえどもこの側面は決して無視できない．低エネルギーで古典化された対象を取り扱う場の量子論の方法として発展してきたK. Wilsonに始まる有効作用の考え方とその重力への適用に，本書の11章が充てられており，Einstein方程式の非幾何学的修正を論ずる終盤の2章に繋がっていく．また，それに先立つ8章では，Einstein方程式そのものの非幾何学的導出法（Deserによるもの等）も紹介されている．
以上を踏まえまとめておこう．本書は，一般相対論と宇宙論をずっと研究してきた，Einstein方程式をこよなく愛する専門家には書けない教科書である．この「思い切りの良さ」こそが本書の最大の魅力であろう．参考文献は冒頭にまとめられてはいるものの，より充実させたものを各章ごとに丁寧に挙げて欲しかった．特に8章以降の著者による要約をさらに深く理解したいと思う読者にとって，文献の適切な引用は不可欠だと思う．
（2019年2月11日原稿受付）

ページの頭に戻る

政池　明

京都大学学術出版会，京都，2018，xx＋442p，23×16 cm，本体4,800円［広い読者向］ISBN 978-4-8140-0155-2

小長谷大介（龍谷大経営）

荒勝文策（1890-1973）は戦前・戦中期の日本で活躍した原子核物理学者である．近年では，太平洋戦争時の原爆研究の一つとされるF研究を率いた人物として知られる．荒勝を主題とした科学史研究がほとんど見られなかったなかで，本書は彼を中心人物とおいて日本の原子核研究の黎明期を記録した待望の書である．
本書はまず荒勝の研究人生の大半を追う．兵庫県に生まれた荒勝は東京高等師範学校を卒業して一旦は教職に就くが，1915年に京都帝国大学（京大）理科大学に入学し，物理研究の道に進むことになる．木村正路の下で実験研究を始め，1918年に京大卒業後そのまま同大学講師となり，3年後に助教授に昇任した．欧州での在外研究に赴いた後，1928年には台北帝国大学の物理学講座の教授に就任している．台北ではコッククロフト・ウォルトン型の高電圧加速器の建設に携わり，加速した陽子を用いたアジア初の人工原子核反応を成し遂げた．1936年に助手の木村毅一らを連れて京大に転任し，物理学第4講座の教授となった荒勝は台北時代よりさらに高エネルギーで荷電粒子を加速できる高電圧加速器を建設し，γ線を用いる原子核反応の研究を進めた．1940年代前半にはサイクロトロン加速器の建設も手がけた．
原子核の諸現象を研究していた荒勝グループは太平洋戦争下で原爆の基礎研究と接点をもつようになる．理研の仁科芳雄たちは陸軍のニ号研究に関与していくが，京大の荒勝たちは海軍のF研究に関わる．F研究は荒勝を主任として，湯川秀樹，木村毅一，清水栄ら京大関係者が名前を連ねていた．近年発見された清水のノートからは遠心分離法の研究や遠心分離器の設計などが明らかにされている．F研究の活動や会合日程は清水日記（清水家所蔵），湯川日記（京大湯川記念館史料室収蔵）などからも確認されており，第4章はF研究を知る貴重な資料となる．
終戦前後以降はいくつかの事象を中心に描かれる．一つは広島と長崎への原爆投下にかかわるものである．荒勝グループが行った広島の第一次・第二次原爆調査（1945年8月），第三次調査（同年9月），長崎の調査（翌年11月）が詳細に語られ，枕崎台風の被災により花谷暉一ら多くの犠牲者が出た第三次調査時の「大野浦の悲劇」も詳述されている．さらに一つは終戦後の占領軍下にある日本で起きたサイクロトロン破壊である．GHQの指示の混乱で起こったとされる1945年11月の理研，阪大，京大のサイクロトロン破壊は広く知られるものの，第9章は荒勝日誌，清水日記，連合国軍の通訳だったトーマス・スミスの回想録を通して，京大での破壊の実態を克明に追っている．破壊時に没収された荒勝研究室の研究ノート類の一部が60年以上を経て米国議会図書館で発見されたエピソードも加わる．
荒勝は原子核に関する諸事件で知られる存在でありながら，日本の科学史上で主要な分析対象からは外れていた．その荒勝の研究人生を繙く機会を本書は与えてくれる．二編構成の本書では，第1編「通史」のなかに日記・日誌類などの豊富な資料の紹介が含まれるのに加えて，第2編「資料」では第1編で触れた資料の一部が全文収録されている．日本の原子核関連の歴史資料集の一つとしても活用できる．戦前・戦中・戦後という激動の時代にあった荒勝たちの活動や思いは，現代社会におかれた物理研究の諸課題を考えるのに有用な材料となるに違いない．
（2019年2月12日原稿受付）

ページの頭に戻る